工程和利润问题

（1）掌握工程问题的三种考法与对应解题步骤，以及常用的赋值方法。

（2）掌握与售价、成本、利润、折扣、利润率等相关的公式。

（3）掌握函数最值问题的两点式。

一、工程问题

【例 1】（2021 广东）为支持“一带一路”建设，某公司派出甲、乙两队工
程人员出国参与一个高铁建设项目。如果由甲队单独施工，200 天可完成该项目；
如果由乙队单独施工，则需要 300 天。甲、乙两队共同施工 60 天后，甲队被临
时调离，由乙队单独完成剩余任务，则完成该项目共需多少天？
    A.120 B.150
    C.180 D.210
【解析】例 1.工程问题，“200 天可完成该项目；如果由乙队单独施工，则
需要 300 天”，给了两个完工时间，属于给完工时间型工程问题。（1）赋总量：
赋总量为 200、300 的公倍数 600。（2）求效率：甲效率=600/200=3，乙效率
=600/300=2。（3）再做题：“甲、乙两队共同施工 60 天后，甲队被临时调离，由
乙队单独完成剩余任务”，假设乙单独的时间为 t，列式：（3+2）*60+2t=600，
解得 t=150，此时容易错选 B 项；注意问的是完成该项目共需多少天，所求
=60+150=210，对应 D 项。【选 D】

【例 3】（2021 北京）农场使用甲、乙两款收割机各 1 台收割一片麦田。已
知甲的效率比乙高 25%，如安排甲先工作 3 小时后乙加入，则再工作 18 小时就
可以完成收割任务。问如果增加 1 台效率比甲高 40%的丙，3 台收割机同时开始
工作，完成收割任务的用时在以下哪个范围内？
    A.8 小时以内 B.8～10 小时之间
    C.10～12 小时之间 D.12 小时以上
【解析】例 3.属于给效率比例型的工程问题，“已知甲的效率比乙高 25%”，
25%=1/4，推出效率比甲/乙=5/4；（1）赋效率：赋值甲的效率=5，乙的效率=4；
“增加 1 台效率比甲高 40%的丙”，丙效率=5*（1+40%）=7。（2）求总量：“如
安排甲先工作 3 小时后乙加入，则再工作 18 小时就可以完成收割任务”，总量
=5*3+（5+4）*18=177。（3）再做题：三台一起做，t=177/（5+4+7）=177/16=11+，
对应 C 项。【选 C】

【例 6】（2020 江苏）某装配式建筑企业接到一个生产 1033 套楼板的订单。
甲班组生产 5 天后，乙班组再生产 4 天，刚好完成任务。若甲班组比乙班组每天
多生产 23 套，则甲班组生产楼板的套数是：
    A.625 套 B.645 套
    C.535 套 D.515 套
【解析】例 6.工程问题，给了时间，还给了总量，有具体值，列方程。设
甲的效率为 x，则乙的效率为 x-23，“甲班组生产 5 天后，乙班组再生产 4 天，
刚好完成任务”，列式：5x+4*（x-23）=1033，解得 x=125，问甲总共生产的套
数，所求=5x=625，对应 A 项。【选 A】

【解析】拓展.工程问题，给了多个完工时间，可以赋总量，求效率，列式
求解；赋值一个订单的总量为 60，则赵、钱、孙、李的效率分别为 3、3、4、5。
“三个订单同时完工且用时最短”，同时开始同时结束，先总体，确定总的工作
时间，t=（3*60）/（3+3+4+5）=180/15=12 小时。按人头分析工作量，问帮谁，
就分析谁；问赵协助钱的时间，60 的工作量，钱一直在工作，钱工作量为 3*12=36，
剩余的 60-36=24 是赵的工作量，赵协助钱的工作时间=24/3=8 小时，对应 A 项。
【选 A】

【拓展】（2019 联考）某河道由于淤泥堆积影响到船只航行安全，现由工程
队使用挖沙机进行清淤工作，清淤时上游河水又会带来新的泥沙。若使用 1 台挖
沙机 300 天可完成清淤工作，使用 2 台挖沙机 100 天可完成清淤工作。为了尽快
让河道恢复使用，上级部门要求工程队 25 天内完成河道的全部清淤工作，那么
工程队至少要有多少台挖沙机同时工作？
    A.4 B.5
    C.6 D.7
【解析】拓展.挖沙机相当于牛，泥沙相当于草，属于牛吃草问题。利用公
式：草每天生长的量=（300*1-100*2）/（300-100）=0.5；默认挖沙机的效率都
为 1，原来草量=（1-0.5）*300=150，假设现在有 x 台挖沙机，150=（x-0.5）
*25，解得 x=6.5，6.5 台刚好能完成，挖沙机必须是整数，至少需要 7 台挖沙机，
对应 D 项。【选 D】

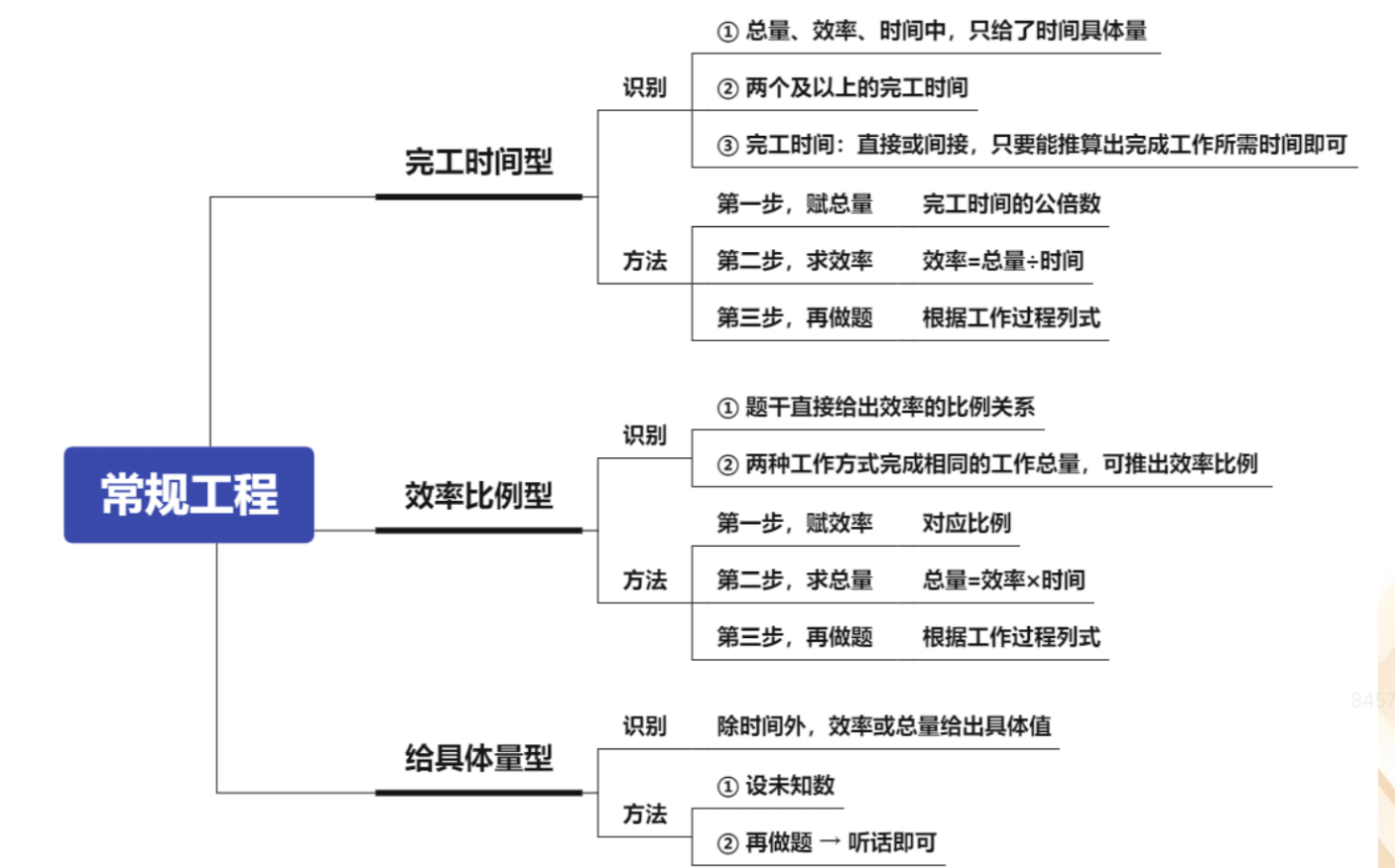
1.完工时间型：
    （1）识别：总量、效率、时间，只给了时间具体量；两个及两个以上的完
工时间；完工时间：直接或间接，只要能推算出完成工作所需时间即可。
    （2）方法：第一步：赋总量，完工时间的公倍数；第二步：求效率，效率=
总量/时间；第三步：再做题，根据工作过程列式。
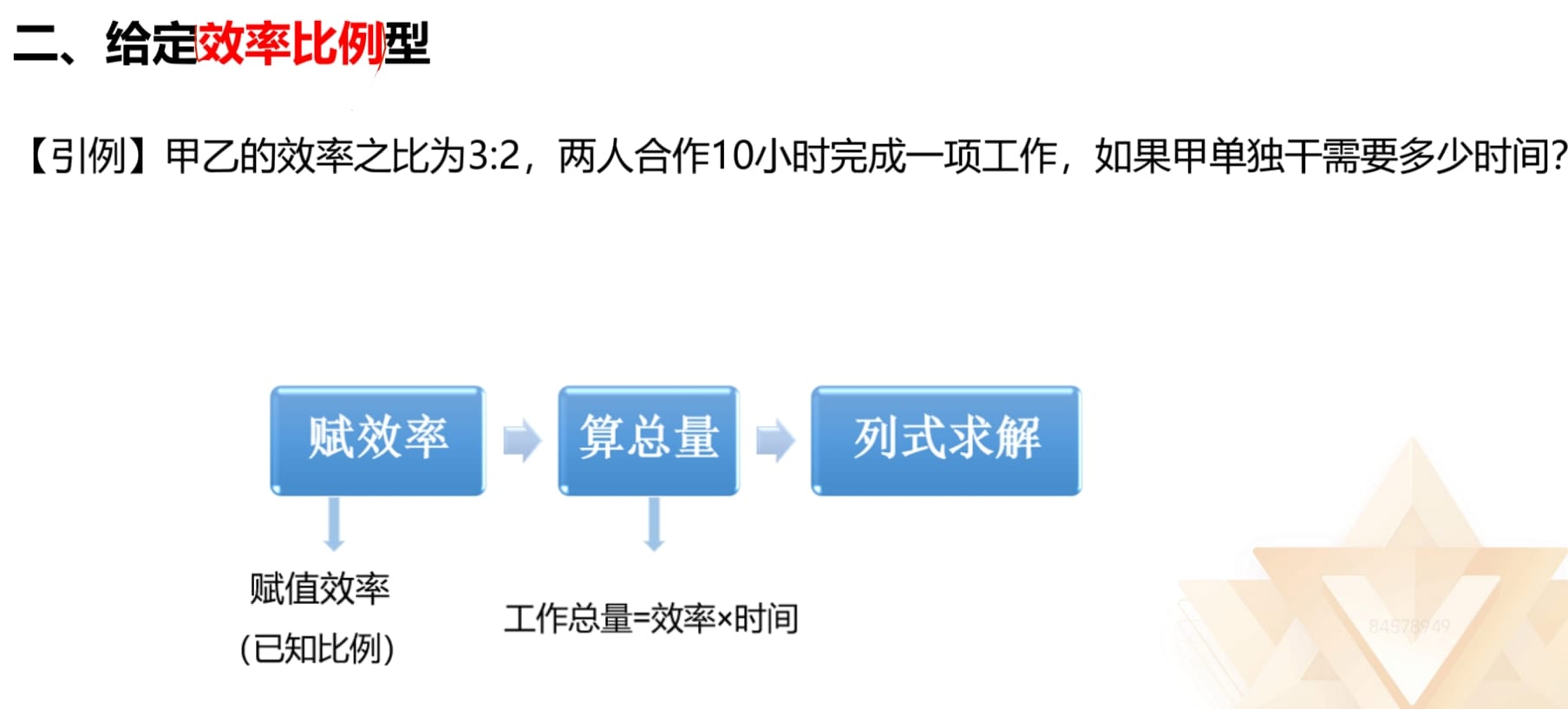
2.效率比例型：
    （1）识别：题干直接给出效率的比例关系；两种工作方式完成相同的工作
总量，可推出效率比例。
    （2）方法：第一步：赋效率，对应比例；第二步：求总量，总量=效率*时
间；第三步：再做题，根据工作过程列式。
3.给具体量型：
    （1）识别：除时间外，效率或总量给出具体值。
    （2）方法：设未知数；再做题→听话即可。

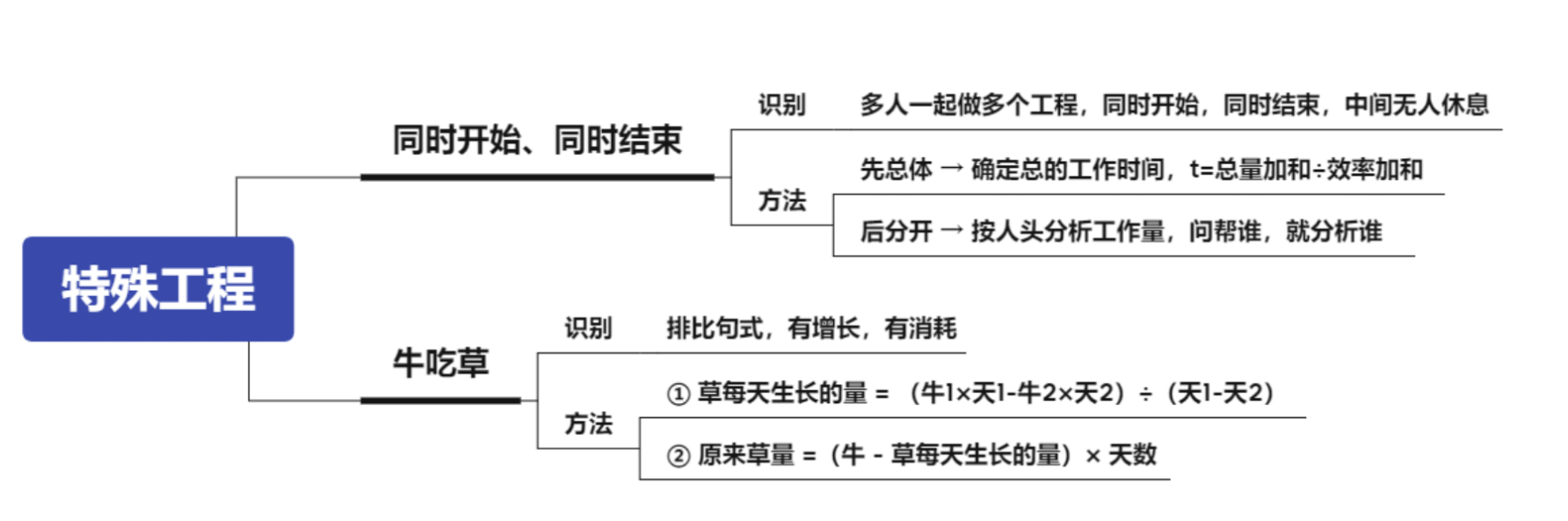
1.同时开始，同时结束：
    （1）识别：多人一起做多个工程，同时开始，同时结束，中间无人休息。
    （2）方法：
        ①先总体→确定总的工作总量，t=总量加和/效率加和。
        ②后分开→按人头分析工作量，问帮谁，就分析谁。
2.牛吃草：
    （1）识别：排比句式，有增长，有消耗。
    （2）方法：
        ①草每天生长的量=（牛 1*天 1-牛 2*天 2）/（天 1-天 2）。
        ②原来草量=（牛-草每天生长的量）*天数。

二、经济利润问题

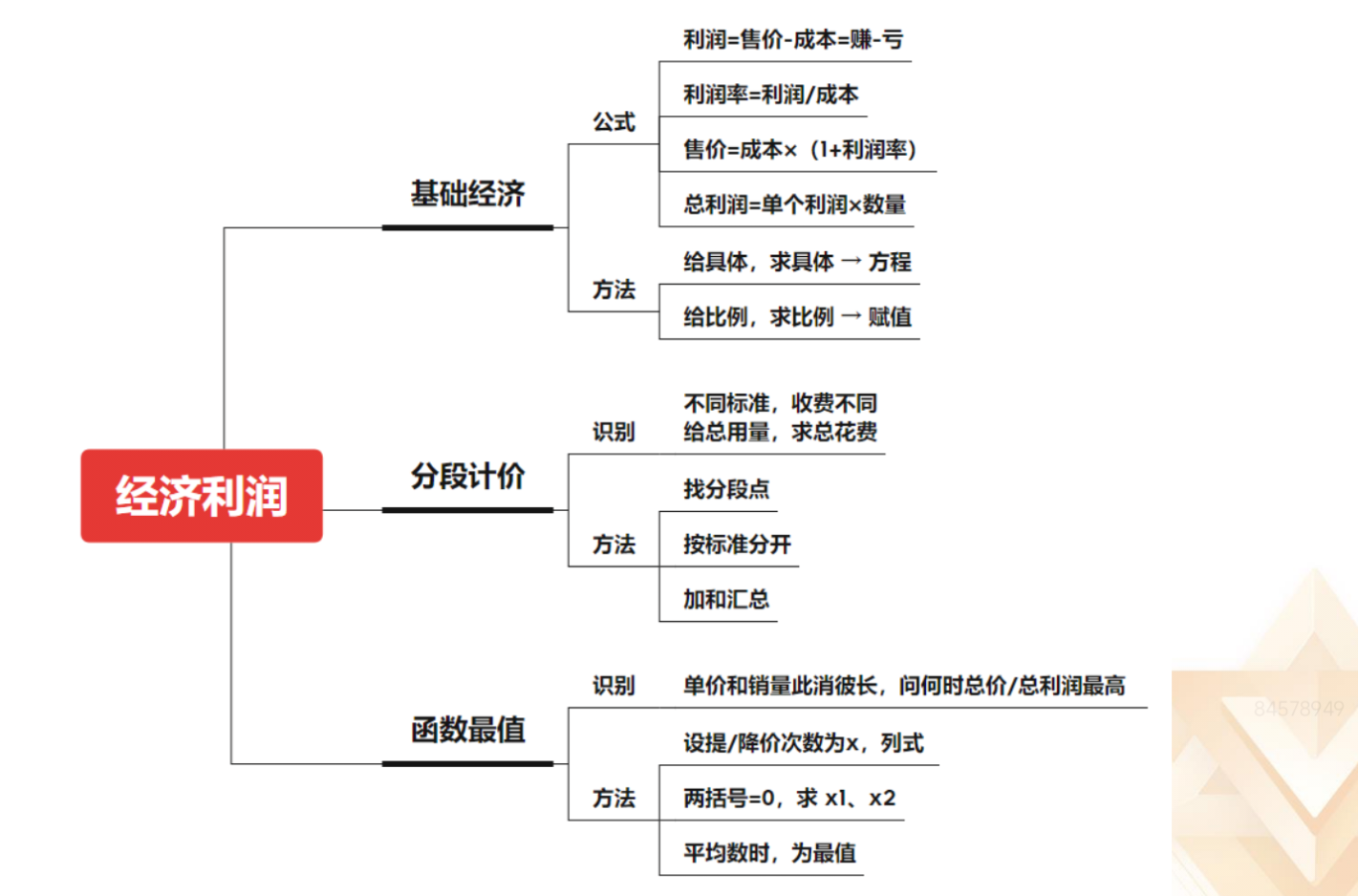
1.基础经济：
    （1）公式：利润=售价-成本=赚-亏；利润率=利润/成本；售价=成本*（1+
利润率）；总利润=单个利润*数量。
    （2）方法：给具体，求具体→方程；给比例求比例→赋值。
2.分段计价：
    （1）识别：不同标准，收费不同；给总用量，求总花费。
    （2）方法：找分段点，按标准分开，加和汇总。
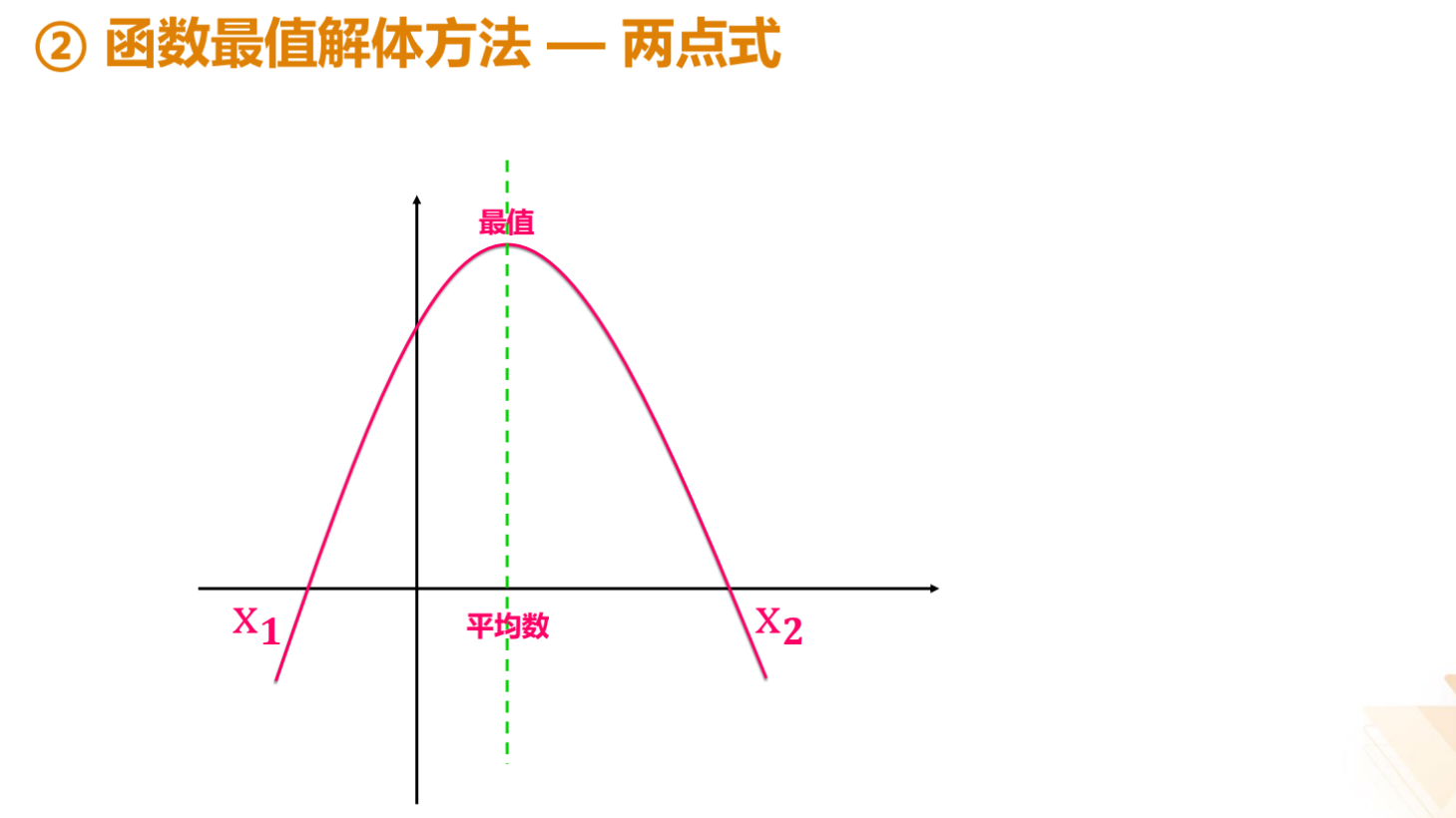
3.函数最值：
    （1）识别：单价和销量此消彼长，问何时总价/最利润最高。
    （2）方法：设提/降价次数为 x，列式；两括号=0，求 x1、x2；平均数时，
为最值。

三、补充内容

知识点检测

1.知识点检测：
    （1）工程问题的基本等量关系：总量=效率*时间。
    （2）给完工时间型工程问题的解题思路：先赋值总量，赋值的技巧是找公
倍数（最好是最小公倍数）；再算效率=总量/时间；最后根据工程过程列式子或
方程。
    （3）给效率比例型工程问题的解题思路：先赋值效率，赋值的技巧是赋值
比例数；再算总量=效率*时间；最后根据工程过程列式子或方程。
    （4）给具体量型工程问题的解题思路：设未知数，找等量关系列方程。
    （5）经济利润问题涉及的基本公式：利润=售价-进价（利润=赚-亏，但是
不建议用）、利润率=利润/成本、折扣=售价/原价、总价=单价*个数。该题型常
用的方法：方程（给具体量求具体量）、赋值（给比例求比例）。
    （6）典型的分段计价问题包括水电费、出租车费、税费等，其解题过程：
分段计算、汇总加和。
    （7）函数最值问题的题型特征：单价和数量此消彼长，求最高利润或总价；
解题方法：①列式；②解 x1、x2；③求平均数。