排列组合、概率问题与容斥原理
Last updated on
Jun 26, 2024
一、排列组合 1.分类与分步:单独拿出一个步骤,如果可以完成这件事,就是分类;如
果不能完成这件事,必须所有步骤都完成,就是分步。
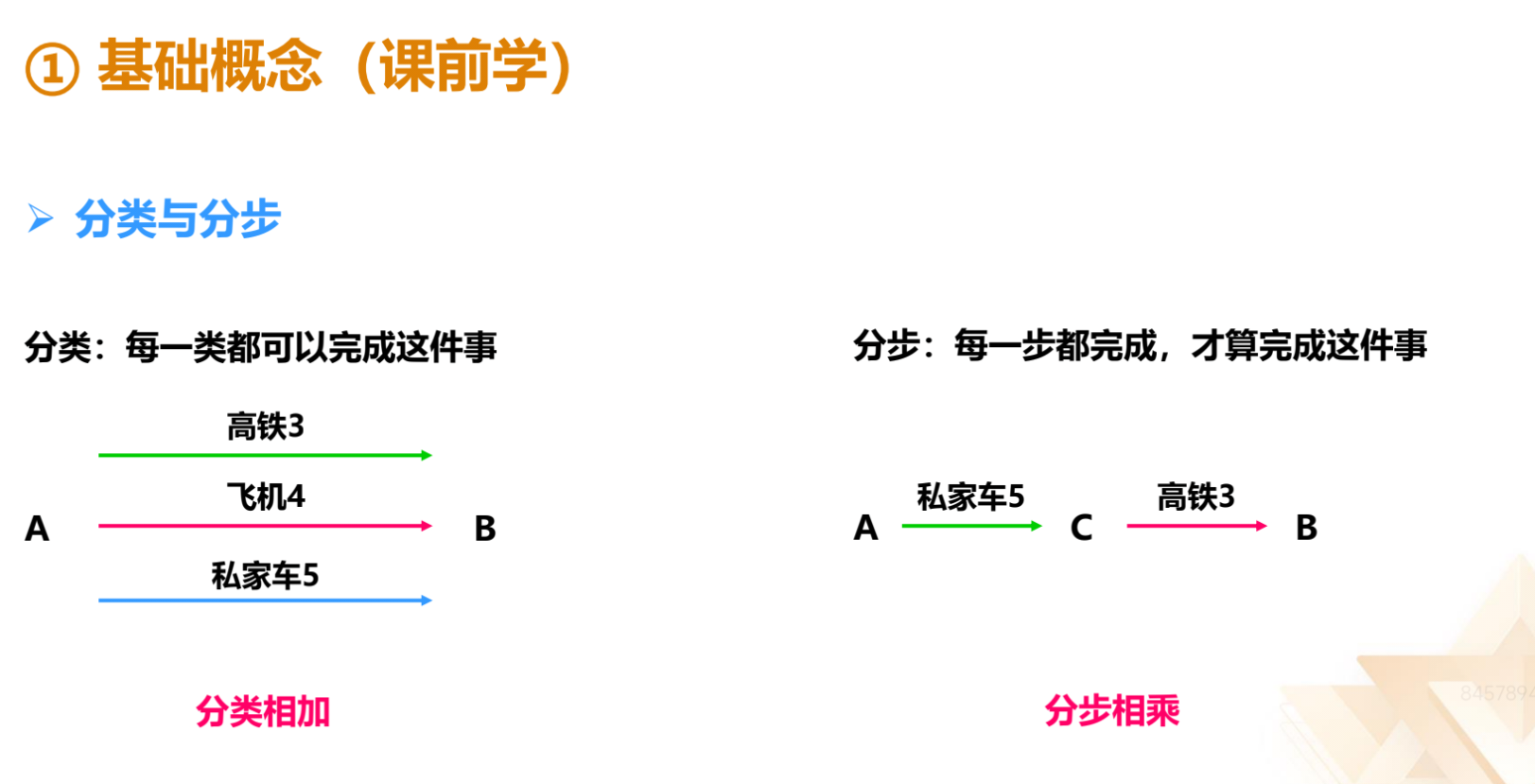
(1)分类:每一类都可以完成这件事。例:从 A 地到 B 地可以选择高铁
(3 种选择)、飞机(4 种选择)、私家车(5 种选择),问从 A 地到 B 有有
多少种选择?
答:每一种交通工具都可以从 A 地到 B 地,为分类,用相加:3+4+5=12。
(2)分步:每一步都完成,才算完成这件事。
例:从 A 地到 B 地需要经过 C 地中转,单独开私家车无法到达 B 地,分为
两步进行,必须先从 A 地到 C 地,再从 C 地到 B 地,只有每一步都完成,才能
从 A 到 B,为分步。
(3)例:每天早晨起来都是拥抱太阳,打开衣柜以后,有 2 件上衣、3
条裤子、2 双鞋,问今天的服装搭配有多少种。单独穿 1 件穿上衣或者 1 条裤
子或 1 双鞋,都无法完成穿衣服这件事,所以穿衣服这件事是分步,穿上衣、
裤子、鞋都要完成。
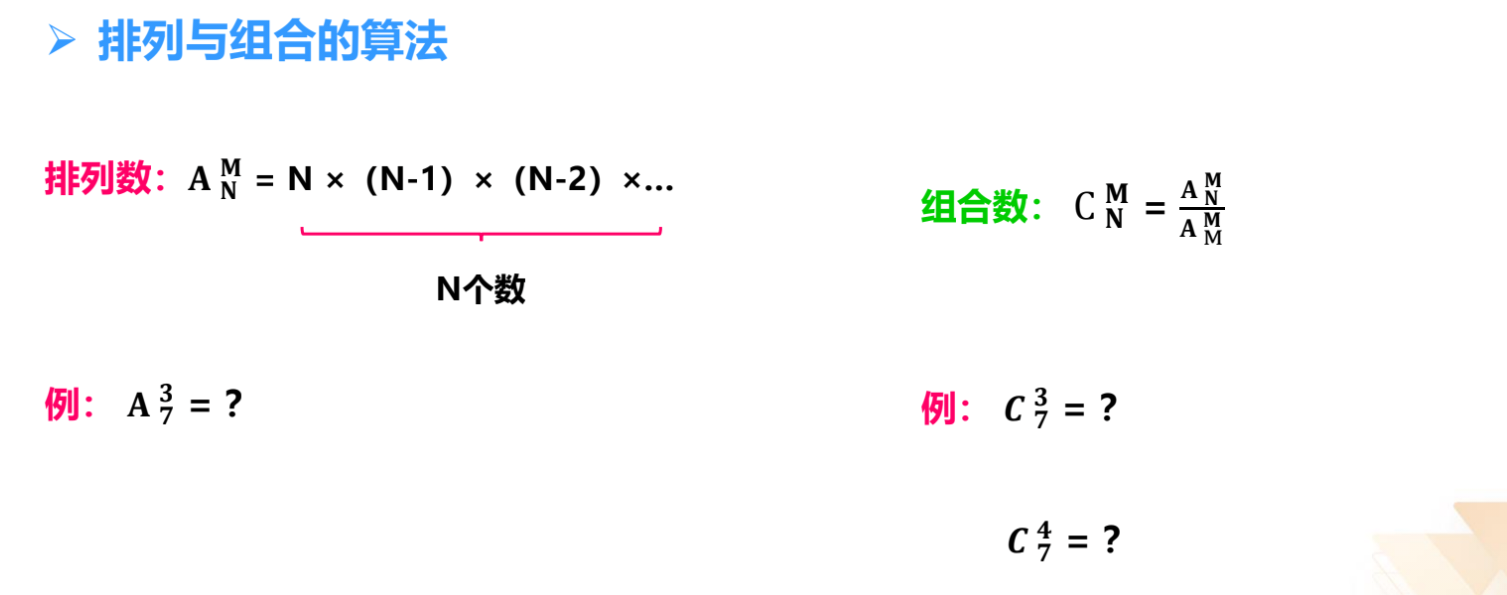
排列与组合:评判的依据是看调换顺序对结果有没有影响。
(1)排列:选取元素的顺序对于结果有影响,用 A 表示。
①常见于:排队、排序的题干环境。
②例:从大美圆、野狼志、鸡汤照、粤语涛、美食熙中,选出 2 人,第一
人教你言语,第二人教你数资。
答:假设选出的 2 人为鸡汤照、美食熙,先选鸡汤照教言语,后选美食熙
教数资,鸡汤照不擅长教言语,美食熙不擅长教数资,把顺序对调之后鸡汤照
擅长教数资,美食熙擅长教言语,对调顺序对结果有影响,用排列,用 A(5,2)。
(2)组合:选取元素的顺序对于结果无影响,用 C 表示。
①常见于:选人、确定名单的题干环境。
②例:从大美圆、野狼志、鸡汤照、粤语涛、美食熙中,选出 2 人,教你
学习。
答:从 5 个人中选 2 个人,要先知道选出来是干什么事,本题中的事是“教
你学习”,假设选出的 2 人为鸡汤照、美食熙,先选鸡汤照,后选美食熙,顺
序对调之后结果都是鸡汤照、美食熙陪你学习,即无影响,用组合,为 C(5,2)。
(2020 新疆)某美术馆计划展出 12 幅不同的画,其中有 3 幅油画、
4 幅国画、5 幅水彩画,排成一行陈列,要求同一种类的画必须连在一起,并且
油画不放在两端,问有多少种不同的陈列方式?
A.不到 1 万种 B.1 万~2 万种之间
C.2 万~3 万种之间 D.超过 3 万种
【解析】例 1.出现“必须连在一起”,为相邻问题,考虑捆绑法。已知“要
求同一种类的画必须连在一起”,将 3 幅油画捆绑,内部有顺序,为 A(3,3);
同理,将 4 幅国画捆绑为 A(4,4);将 5 幅水彩画捆绑为 A(5,5)。已知“油
画不放在两端”,油画只能在中间,要么国画在左、水彩画在右,要么水彩画在
左、国画在右,对调顺序对结果有影响,为 A(2,2)。先捆再排,分步用乘法,
所求=A(3,3)*A(4,4)*A(5,5)*A(2,2)=6*24*120*2=720*48>3 万,对应
D 项。【选 D】
(2020 联考)某学习平台的学习内容由观看视频、阅读文章、收藏
分享、论坛交流、考试答题五个部分组成。某学员要先后学完这五个部分,若观
看视频和阅读文章不能连续进行,该学员学习顺序的选择有:
A.24 种 B.72 种
C.96 种 D.120 种
【解析】例 2.“某学员要先后学完这五个部分”,提示有顺序。出现“不
能连续进行”,为不相邻问题,考虑插空法。已知“观看视频和阅读文章不能连
续进行”,观看视频、阅读文章不能相邻。先排收藏分享、论坛交流、考试答题,
内部有顺序,为 A(3,3);3 个部分形成 4 个空,从 4 个空中选出 2 个空,插入
观看视频、阅读文章,调换顺序对结果有影响,为 A(4,2)。先排再插,分步
用乘法,所求=A(3,3)*A(4,2)=6*4*3=72,对应 B 项。【选 B】
二、概率问题 1.基础概念:
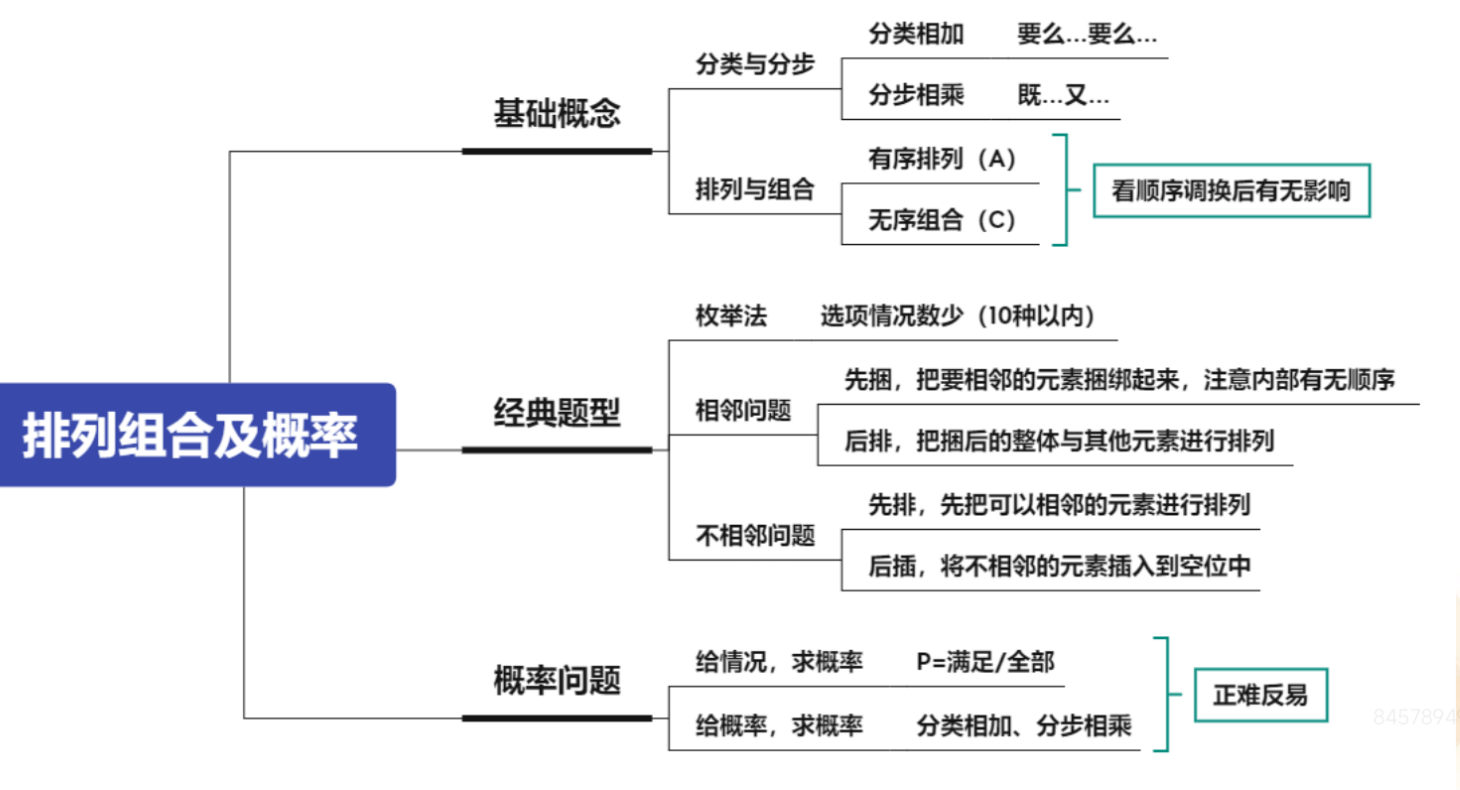
(1)分类与分步:
①分类相加:要么……要么……。
②分步相乘:既……又……。
(2)排列与组合:看顺序调换后有无影响。
①有序排列(A)。
②无序组合(C)。
2.经典题型:
(1)枚举法:选项情况数少(10 种以内)。
(2)相邻问题:
①先捆:把要相邻的元素捆绑起来,注意内部有无顺序。
②后排:把捆后的整体与其他元素进行排列。
(3)不相邻问题:
①先排:先把可以相邻的元素进行排列。
②后插:将不相邻的元素插入到空位中。
3.概率问题:正难反易。
(1)给情况,求概率:P=满足/全部。
(2)给概率,求概率:分类相加、分步相乘。
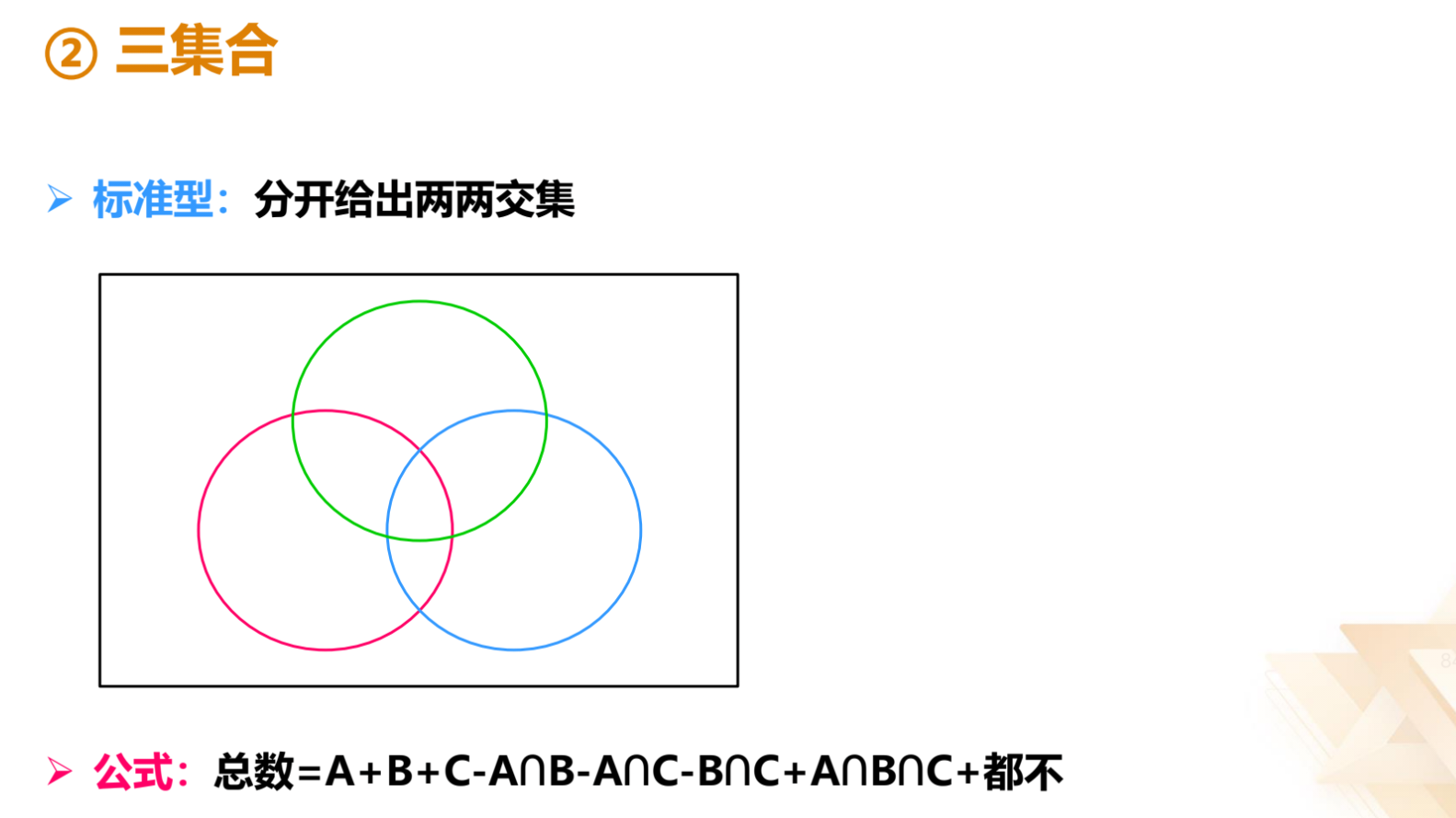
三、容斥原理 标准型:分开给出两两交集。公式:总数=A+B+C-A∩B-A∩C-B∩C+A∩B
∩C+都不。先加和 A+B+C+都不,A∩B、A∩C、B∩C 都加了两次,都需要减去一
次;A∩B∩C 加了三次,减了三次,此时空了,需要加上一次;要做到不重不漏,
总数=A+B+C-A∩B-A∩C-B∩C+A∩B∩C+都不。
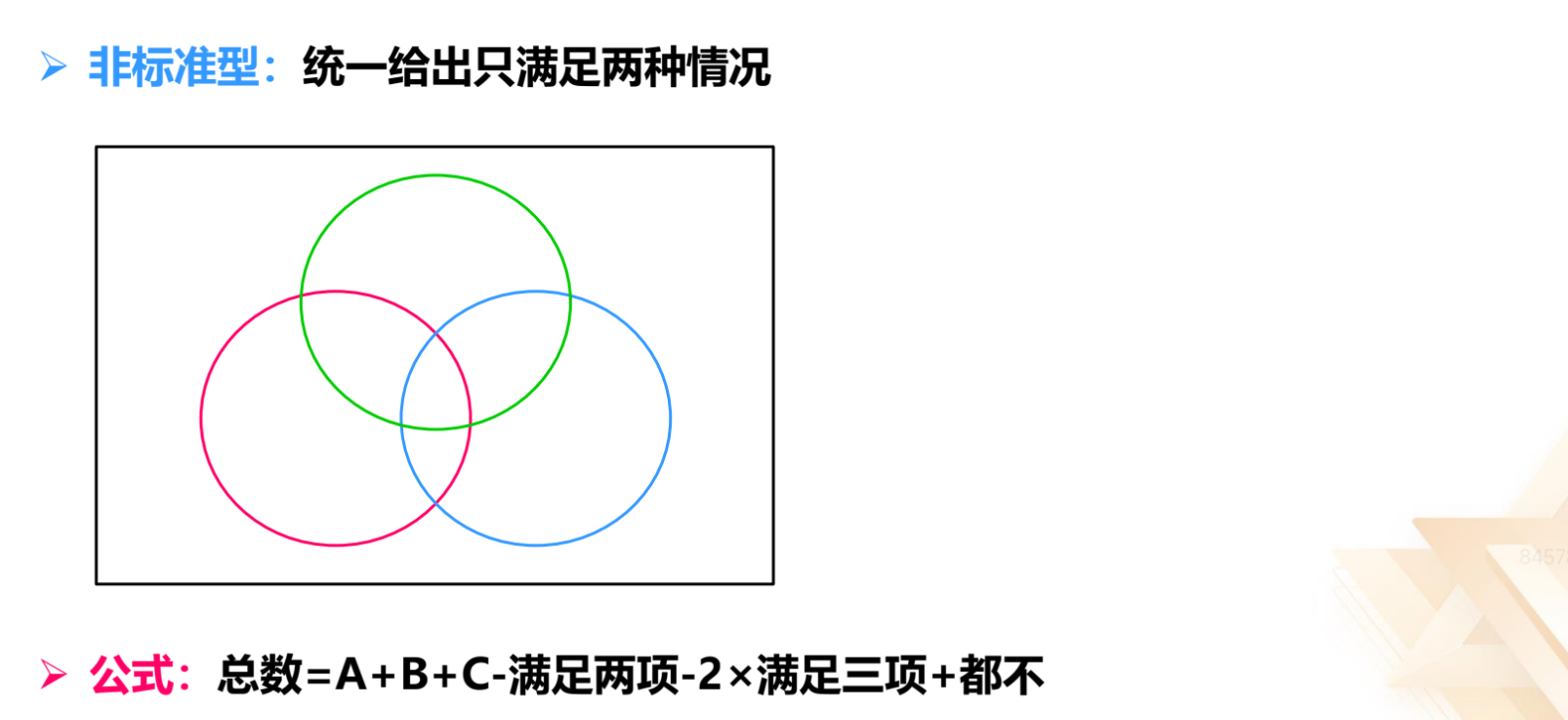
非标准型:统一给出只满足两种情况。公式:总数=A+B+C-满足两项-2*
满足三项+都不。红色阴影部分是只满足两项的部分,先加和 A+B+C,红色阴影
满足两项的部分加了两次,减去一次;三者交集的部分加了三次(△),需要减
去两次;总数=A+B+C-满足两项-2*满足三项+都不。
【注意】容斥问题:不一定考查,但是考查概率很大。
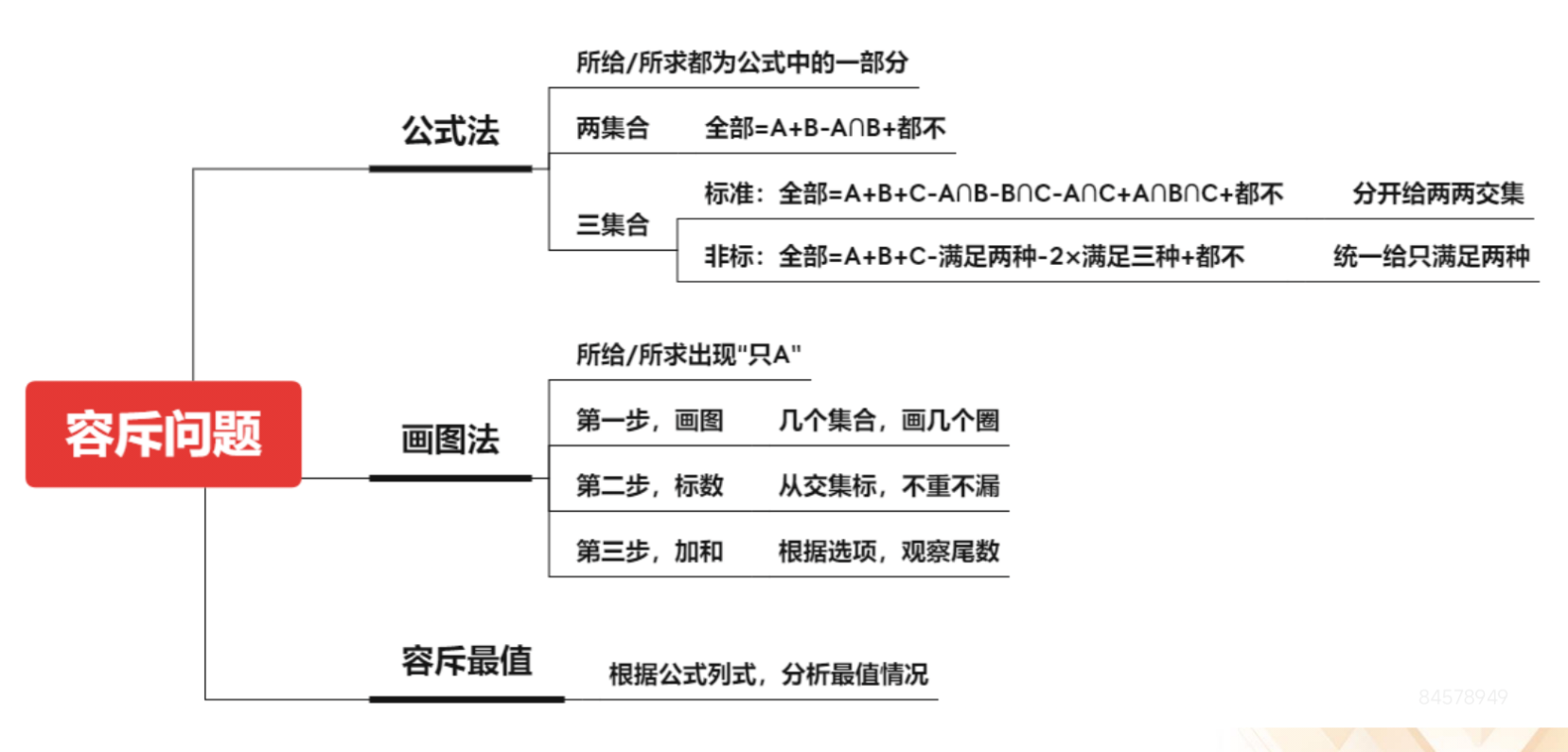
1.公式法:
(1)所给/所求都为公式中的一部分。
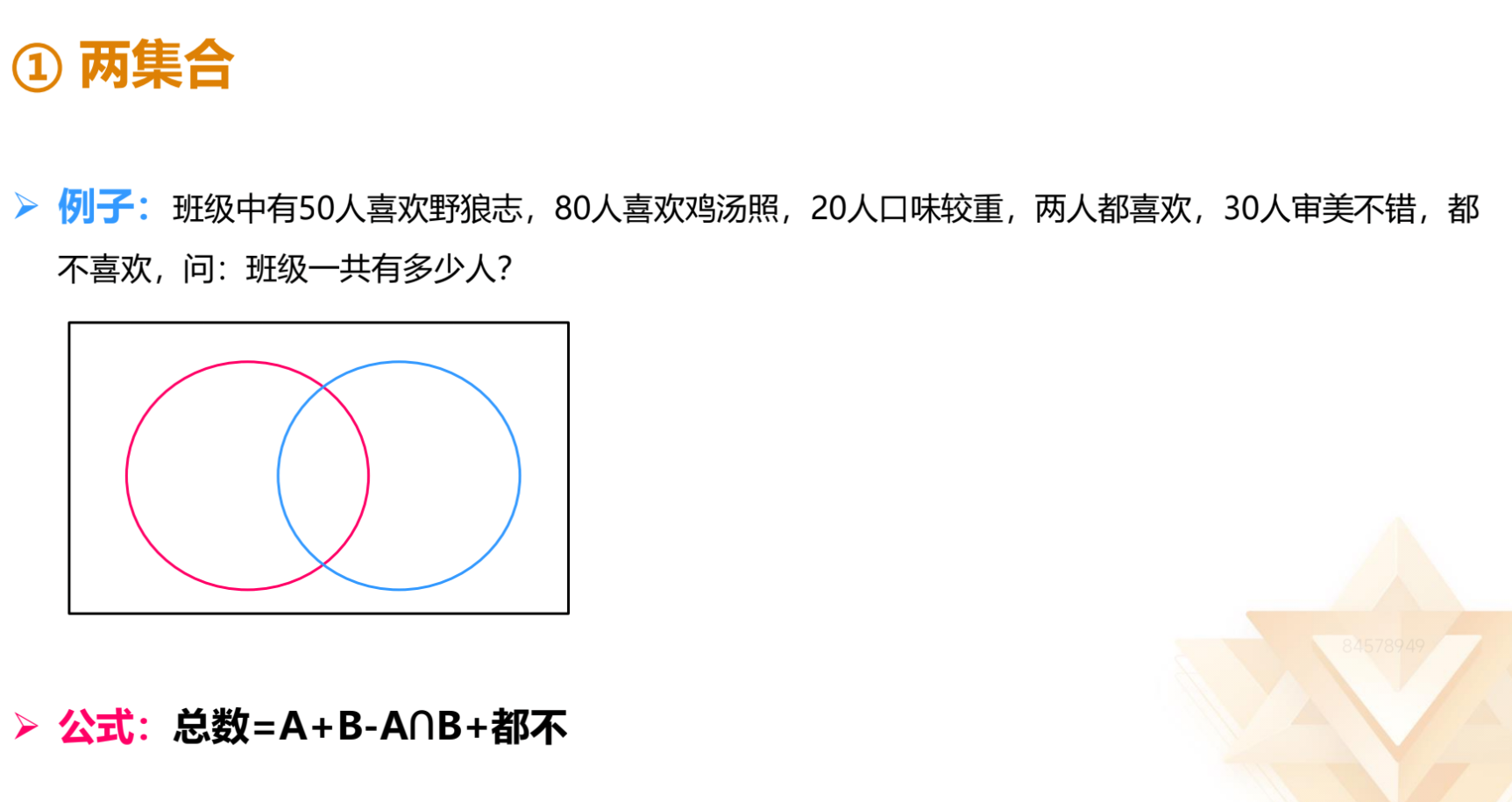
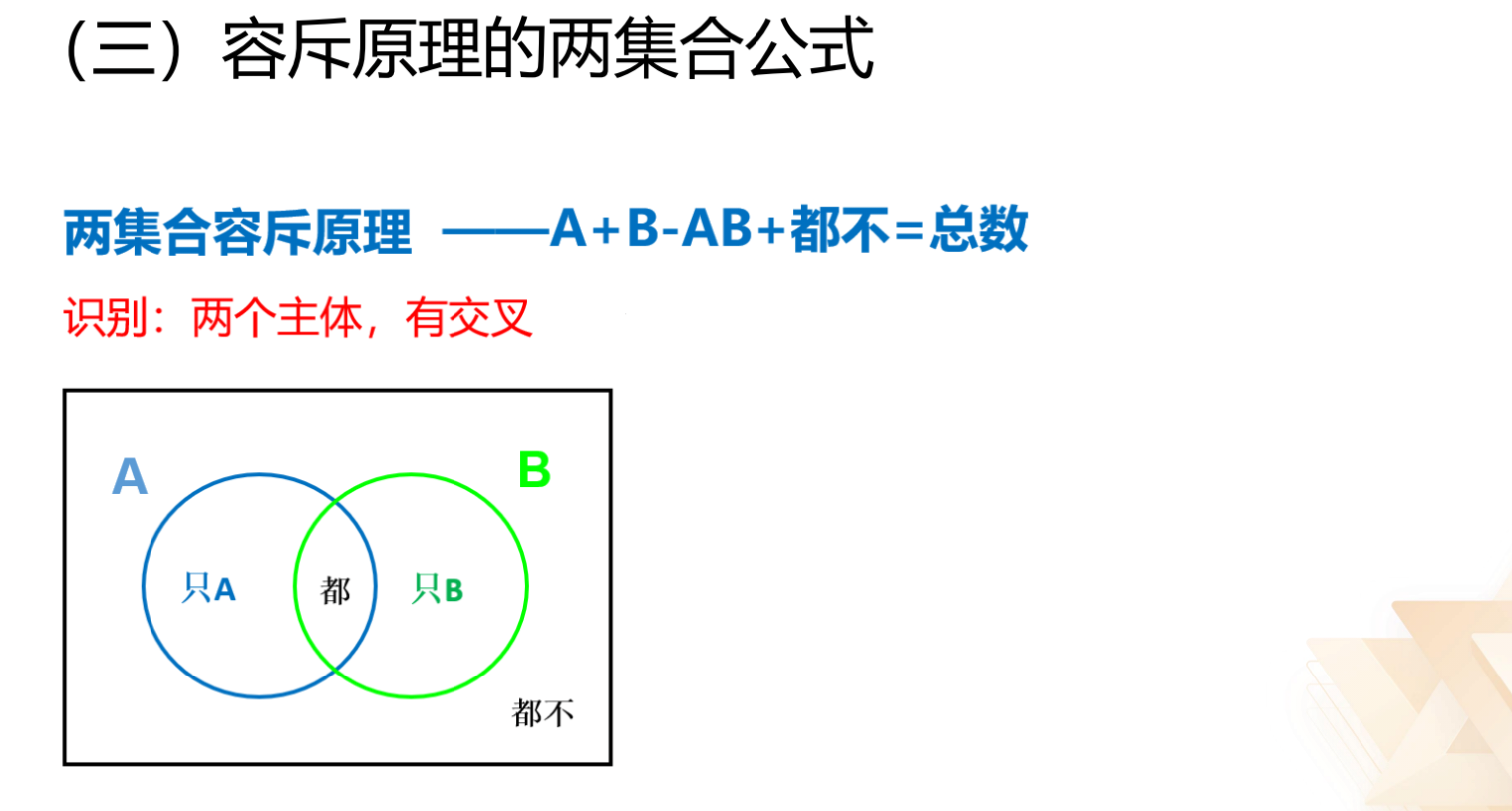
(2)两集合:全部=A+B-A∩B+都不。
(3)三集合:
①标准:全部=A+B+C-A∩B-B∩C-A∩C+A∩B∩C+都不。分开给两两交集。
②非标:全部=A+B+C-满足两种-2*满足三种+都不。统一给只满足两种。
2.画图法:
(1)所给/所求出现“只 A”。
(2)步骤:
①第一步,画图。几个集合,画几个圈。
②第二步,标数。从交集标,不重不漏。
③第三步,加和。根据选项,观察尾数。
3.容斥最值:根据公式列式,分析最值情况。
1.数量关系:要清楚自己能做的题型是哪些,比如工程问题、容斥问题、方
程问题、套路题,这些题型都是可以掌握的,在刷题时针对性刷题,可以工程问
题连续刷 50 道,经济利润问题连续刷 50 道……,一天做 10 道,5 天做一个题
型。
2.资料分析:如果做资料分析慢、正确率不高、提升速度慢,如何有效提升?
(1)先把基础打牢,各种题型的公式、基本概念要熟记之后再刷题。
(2)判定题型慢:当题干特别长的时候,其实并不是题型难判别,只是本
题的主体比较长而已,本质上对于判定题型来说没有影响。要找判断题型的关键
字,比如出现“占”字,就确定为比重问题,再找部分、总体,如果判定题型和
找主体放在一起找,就容易混乱,从而找错数据。
①第一步:先找判定题型的关键字,增长+倍、占、平均。
②第二步:找主体的关键字。
③例:在粉笔年底年终奖增速最高的年份,长得最帅的数资老师其工资占其
收入的比重比长得最高的言语老师高了几个百分点?
读题:先找判别题型的关键字,看到“占”字,是比重问题。谁比谁高了多
少个百分点,是两个主体之间的百分点关系,百分点是由两个比重(百分数)作
差得来的,再对应材料找两个主体,最帅的数资老师是志哥,最高的言语老师是
熙熙,再找对应的数据即可。
(3)方法、技巧、习惯:在课堂上积累自己的做题技巧和习惯,这是提速
的关键。方法精讲上讲的是比较基础的知识点,在强化中会有一些提升。比如求
间隔基期,先求 r 间=17.6%+16.7%+17.6%*16.2%,间隔基期=2314/(1+r 间)。资
料分析一切都是从选项入手,假设选项差距大,分母保留两位,所以在求 r 间时
只 需 要 求 出 首 位 即 可 , 大 致 看 一 眼 , 不 需 要 具 体 计 算 出 是 多 少 , r 间=17.6%+16.7%+17.6%*16.2%,大约是 30%出头的数,则间隔基期=2314/1.3。
(4)细化和复盘:让自己变得更加稳。每天做完题之后要做复盘日记,做
一套复盘的提升效果要远远大于做两套不复盘的提升效果,重点有三个内容:
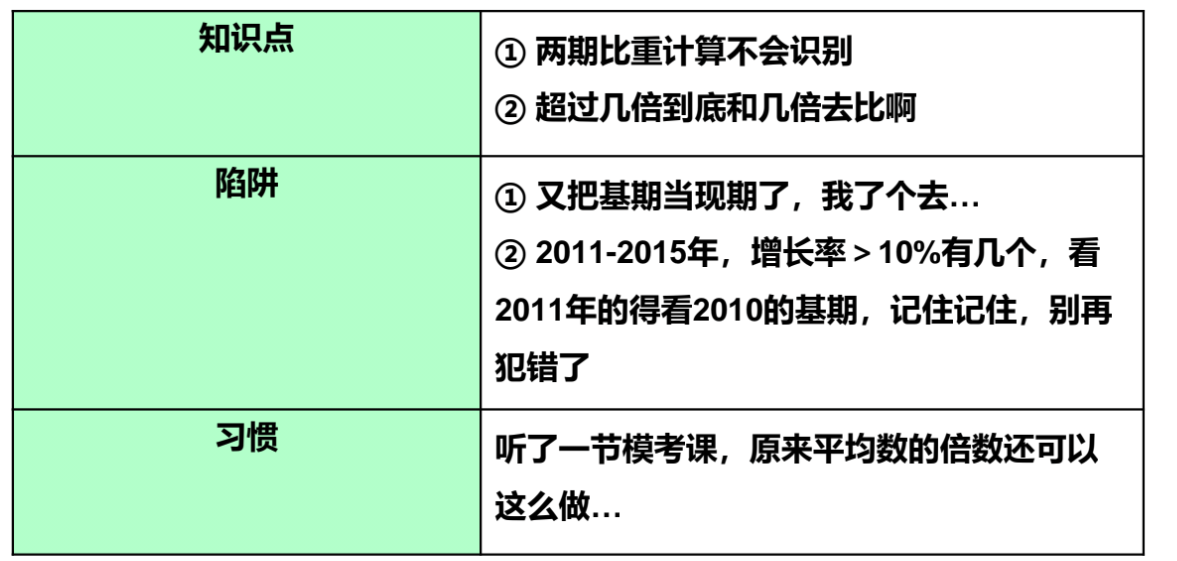
①知识点:分析自己的薄弱知识点,进行针对性提升。
a.两期比重计算不会识别。
b.超过几倍到底和几倍去比啊。如 A 超过 B 的 5 倍,“超过”是大于的意思,
A>B*5→A/B>5,超过几倍就和几倍去比较。
②陷阱:分析自己掉入的陷阱。
a.又把基期当现期了,我了个去……。做题时一定要看清楚时间。
b.2011~2015 年,增长率>10%的有几个,看 2011 年的得看 2010 年的基期,
记住记住,别再犯错了。
③习惯:听了一节模考课,原来平均数的倍数还可以这么做……。如平均数:
A/B÷(C/D),可以看 A/C÷(B/D)。
四、补充内容