强化练习-数量2

Last updated on Aug 22, 2024

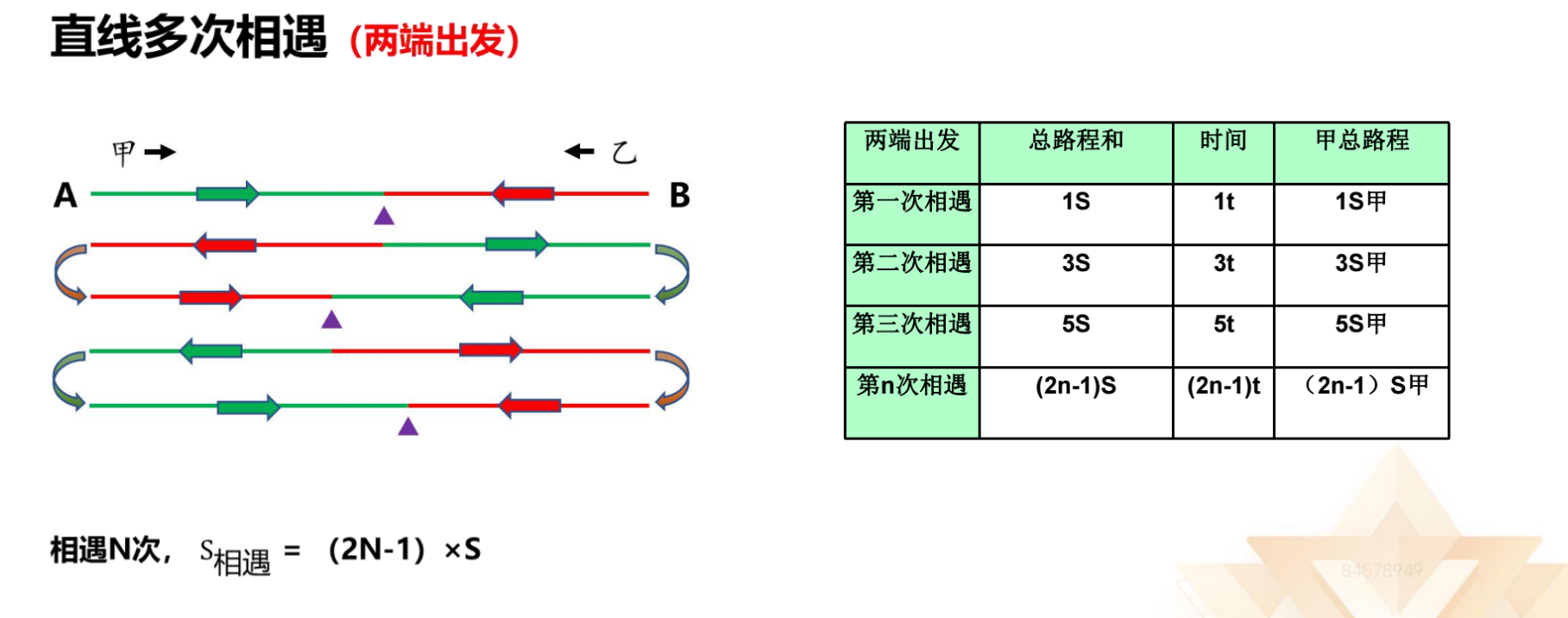
【知识点】直线多次相遇（两端出发）：相遇 N 次，S 相遇=（2N-1）*S。S 和=V
和*T，V 和不变，S 和与 T 成正比，路程之和满足 1：3：5：（2n-1）的关系，时间之
比也满足 1：3：5：（2n-1）的关系，即第一次相遇所用的时间与第二次相遇所用
的时间满足 1：3 的关系。从个体出发，S 甲=V 甲*t，V 甲不变，S 甲与 t 成正比，t
满足 1：3：5：（2n-1）的关系，则 S 甲也满足 1：3：5：（2n-1）的关系，甲走的
路程或乙走的路程满足 1：3：5：（2n-1）的关系。综上，在两端的多次相遇问题
中，不仅是走的总路程，以及每个人走的路程、时间都满足 1：3：5：（2n-1）的
关系


【拓展】（2019 重庆选调）甲、乙两人分别送材料到对方单位，两人同时出
发，各自匀速前进，甲的速度是 2 米/秒，乙的速度是 2.5 米/秒，两人到单位交
材料的时间忽略不计，到达目的地都立即以原速度返回，两人首次在距离甲单位
700 米处相遇，后来又在距离乙单位 525 米处相遇，则甲、乙两个单位相距多少
米？
    A.1575 B.1020
    C.1100 D.720
【解析】拓展.多次相遇问题，题目给第一次相遇的位置，给最终相遇的位
置，求 S 单程。两步走：化比例、画图分析。（1）找比例：第一次相遇甲走了 700
米，第二次相遇甲走了（2*2-1）*700=3*700=2100 米；（2）画图分析：第二次相
遇甲走的路程=S+525 米，2100=S+525→S=1575 米，对应 A 项。【选 A】

【拓展】（2019 新疆兵团）某健身馆准备将一块周长为 100 米的长方形区域
划为瑜伽场地，将一块周长为 160 米的长方形区域划为游泳场馆。若瑜伽场地和
游泳场馆均是满足周长条件下的最大面积。问两块场地面积之差为多少平方米？
    A.625 B.845
    C.975 D.1150
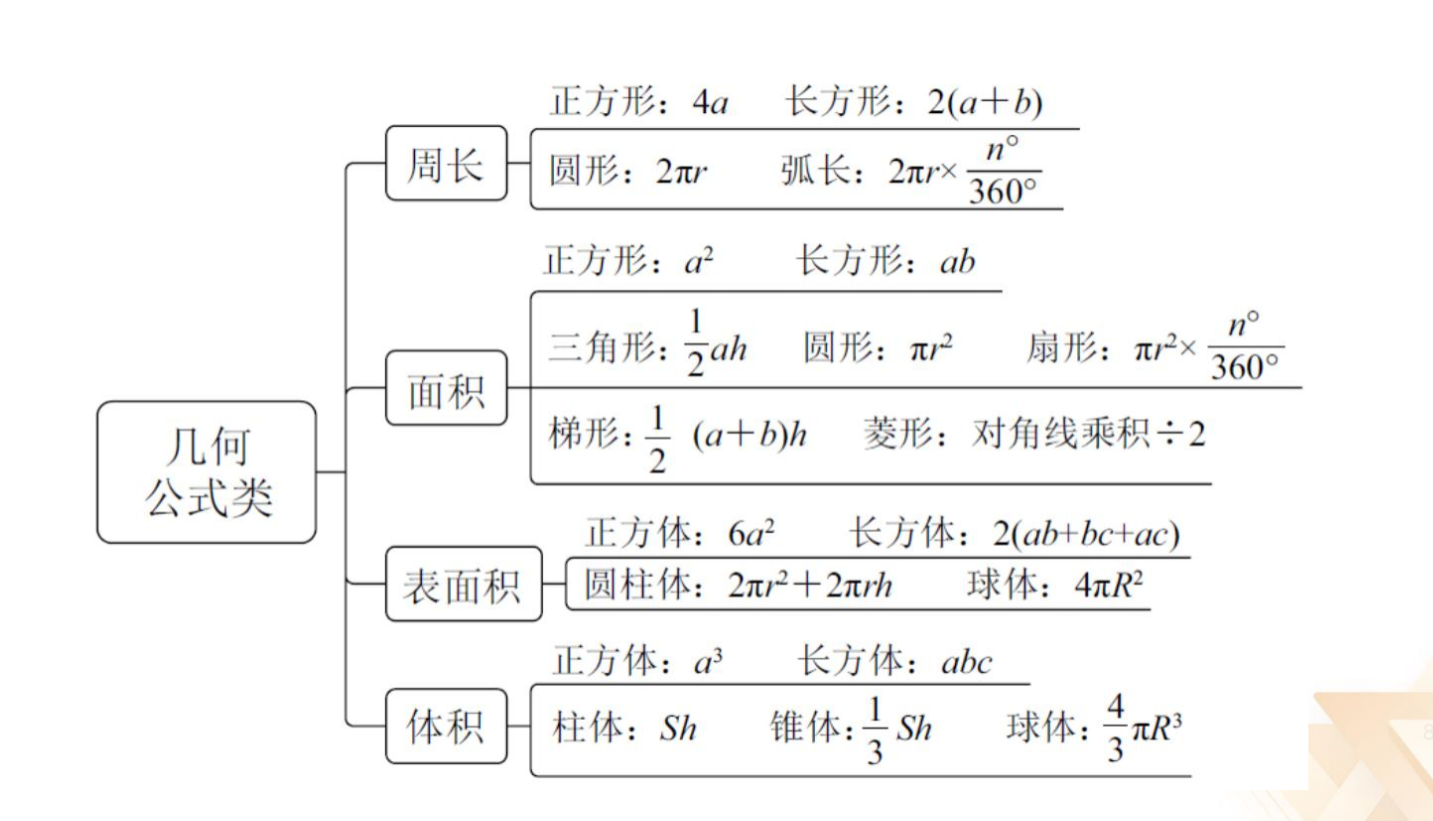
【解析】拓展.当 a+b 一定时，a=b 时，a*b 最大；ab 一定时，a=b，a+b 最
小。当 x=25 时，面积最大，最大值为 25²=625 平方米。同理，当游泳场馆的长
为 40 时，面积最大，最大值为 40²=1600 平方米，所求为 1600-625=975 平方米，
对应 C 项。【选 C】

【拓展】（2018 新疆）某农家要建造一个新的矩形鸡圈，如图所示，该鸡圈
一面靠围墙，另外三面共使用了 200 米长的铁丝网。问如果想让鸡圈的面积最大，
鸡圈的长和宽比值应为多少？
    A.1：1 B.2：1
    C.3：2 D.7：3
【解析】拓展.根据均值不等式：a+2b≥2√2𝑎𝑏，当且仅当 a=2b 时，长方形
的面积最大，即 a：b=2：1，对应 B 项。【选 B】

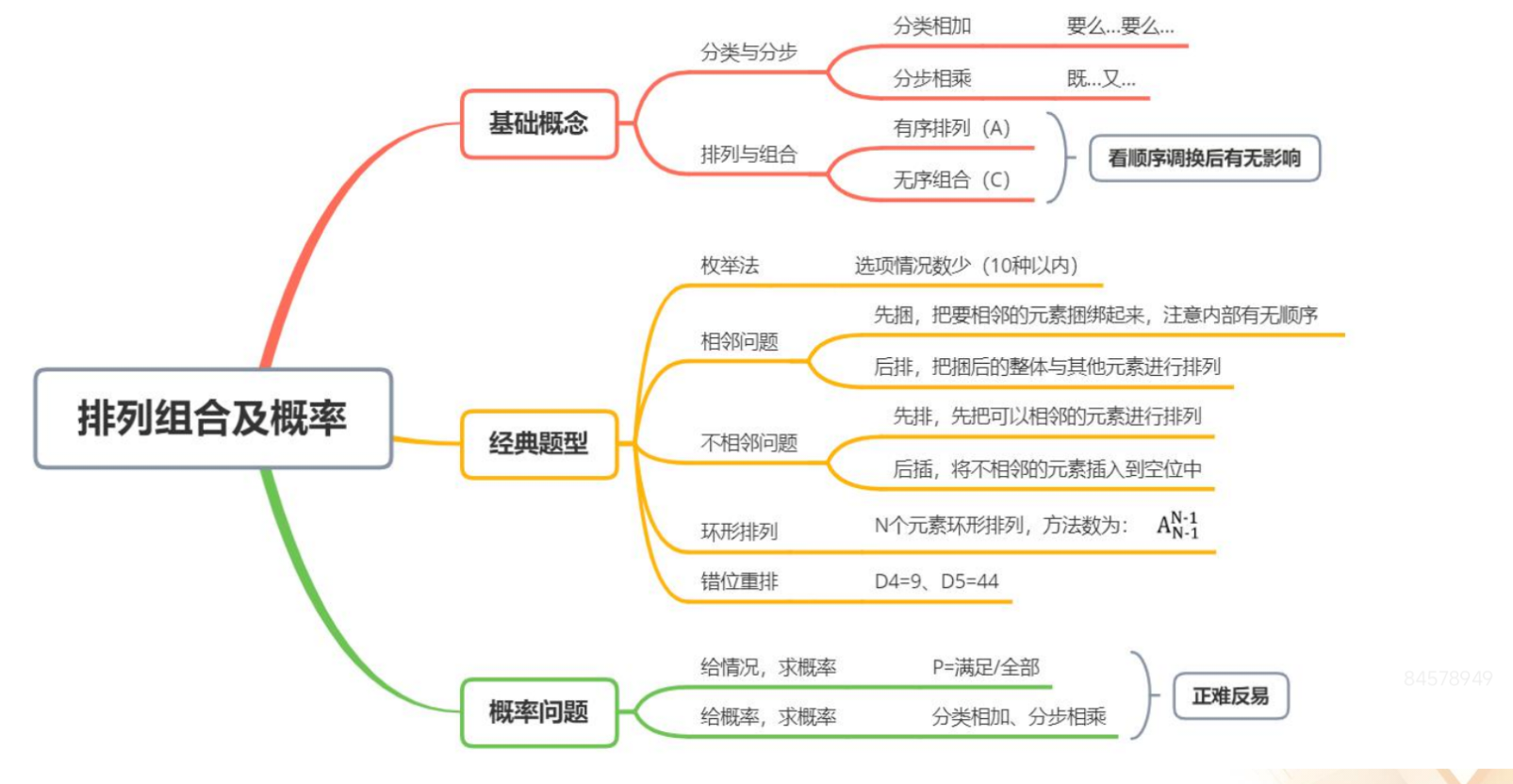
【注意】排列组合及概率：
1.基础概念：
    （1）分类与分步：
        ①分类相加：要么……要么……。
        ②分步相乘：既……又……。
    （2）排列与组合（看顺序调换后有无影响）：
        ①有序排列（A）。
        ②无序组合（C）。
2.经典题型：
    （1）枚举法：选项情况较少（10 种以内）。
    （2）相邻问题：
        ①先捆，把要相邻的元素捆绑起来，注意内部有无顺序。
        ②后排，把捆后的整体与其他元素进行排列。
    （3）不相邻问题：
        ①先排，先把可以相邻的元素进行排列。
        ②后插，将不相邻的元素插入到空位中。
    （4）环形排列：N 个元素环形排列，方法数为：A（N-1,N-1）。如 6 个人直
线排列，为 A（6,6）；6 个人环形排列，为 A（5,5）。若三个人直线排列，可以有
六种情况：ABC、ACB、BAC、BCA、CAB、CBA；三个人环形排列，有三种情况：ABC、
BCA、CAB，这三种情况在 A（6,6）中都有，这三种情况的排列顺序都一样，为 A
（3,3）/3=A（2,2）。
    （5）错位重排：D4=9、D5=44（常考）。
3.概率问题：正难反易。
    （1）给情况，求概率：P=满足/全部。
    （2）给概率，求概率：分类相加、分步相乘。

【注意】跟屁虫问题：
1.识别：两个主体、共同目标求概率。
    （1）例 1：如果甲、乙两人蒙同一选项的概率，甲、乙两人为两个主体，蒙
同一个选项为共同目标，求概率。假设有 A、B、C、D 四个选项，先让甲蒙 B，固
定以后，不用再考虑 B，只需考虑乙和甲蒙同一个选项的概率，乙有四个选项可
以选，只有选择 B 选项时和甲一样，概率为 1/4=25%。
    （2）例 2：从 A 地到 B 地一共有 15 趟车，甲和乙当天乘坐同一趟车的概率
为多少？两个主体，共同目标求概率。假设甲选择了其中一趟，此时甲有 15 趟
车可以选，只有 1 辆车和甲一样，概率为 1/15。
    （3）例 3：假如某班有 174 人，参加篝火晚会，围成一个圈，问甲、乙坐在
一起的概率为多少？先让甲坐一个位置，此时乙有 173 个座位可以选，其中有两
个位座位和甲挨着，概率为 2/173。
2.方法：两个人（物）在一起：先让一个人（物）随便挑，再让第二个人（物）
去找他。

1.例：7 个相同的苹果分给三个小盆友，每人至少分一个，有多少种分法？
答：7 个苹果有 8 个空位，要保证每个小盆友至少分到 1 个，说明板不能插
在两边，所以空位有 6 个；插 1 个板可以分成 2 堆，要分给 3 个小盆友，说明要
插 2 个板，苹果都是一样的，没有顺序，用 C，即 C（6,2）。
2.方法（插板法）：
    （1）N 个元素有（N-1）个空位，分 M 堆，需要（M-1）个板子
    （2）至少分一个共有 C（M-1,N-1）方法，即 C（空,板）。
例：10 个苹果分给 4 个小盆友，每人至少人一个，为 C（9,3）；20 个苹果分
给 5 个小盆友，每人至少分一个，为 C（19,4）。

【知识点】同素分堆：
1.例：10 个相同的苹果分给三个小盆友，每人至少分两个，有多少种分法：
答：可以先给每个小盆友每人分 1 个，再进行分堆。至少分 2 个，即≥2；
≥1+1→≥2。每人分 1 个：10 个苹果拿出 3 个还剩下 7 个，转化为 7 个苹果分
给 3 个小盆友，每人至少分 1 个，则所求=C（6,2）。
2.分法（插板法）：
（1）至少 2 个，先每人分 2-1=1 个。
（2）再按照至少分 1 个分。

【解析】拓展.三局两胜制即谁获得两局胜利，比赛就自动结束。甲要赢，
需要甲赢 2 局，乙赢 1 局。一共分为三种情况：（1）甲、甲、乙；（2）甲、乙、
甲；（3）乙、甲、甲。甲赢的概率是 80%，甲作为优势方，甲要想战胜乙，局数
越多赢的概率越多；说明概率要大于打一局的概率（80%），排除 A、B 项。剩两
个选项随便猜 1 个。【选 C】
【注意】拳击比赛，志哥获胜的概率为 10%，泰森获胜的概率为 90%，如果
打比赛，对于泰森来讲，比的场次越多，赢的概率会大于 90%。

1.公式法：所给/所求为公式中的一部分。
    （1）两集合：全部=A+B-A∩B+都不。
    （2）三集合：
        ①标准：全部=A+B+C-A∩B-B∩C-A∩C+A∩B∩C+都不。
        ②非标：全部=A+B+C-满足两种-2*满足三种+都不。
        ③常识（用得少）：全部=满足一种+满足两种+满足三种+都不（如在某班级
中，报名足球、篮球、排球运动会，一定存在有报 1 个、2 个、3 个的，全部=满
足一种+满足两种+满足三种）。
2.画图法：所给/所求出现“只 A”（只满足某一种主体）。
    （1）第一步，画圈。几个集合，画几个圈。
    （2）第二步，标数。从交集标，不重不漏。
    （3）第三步，加和。根据选项，观察尾数。
3.容斥最值（考查最多）：根据公式列式，分析最值情况

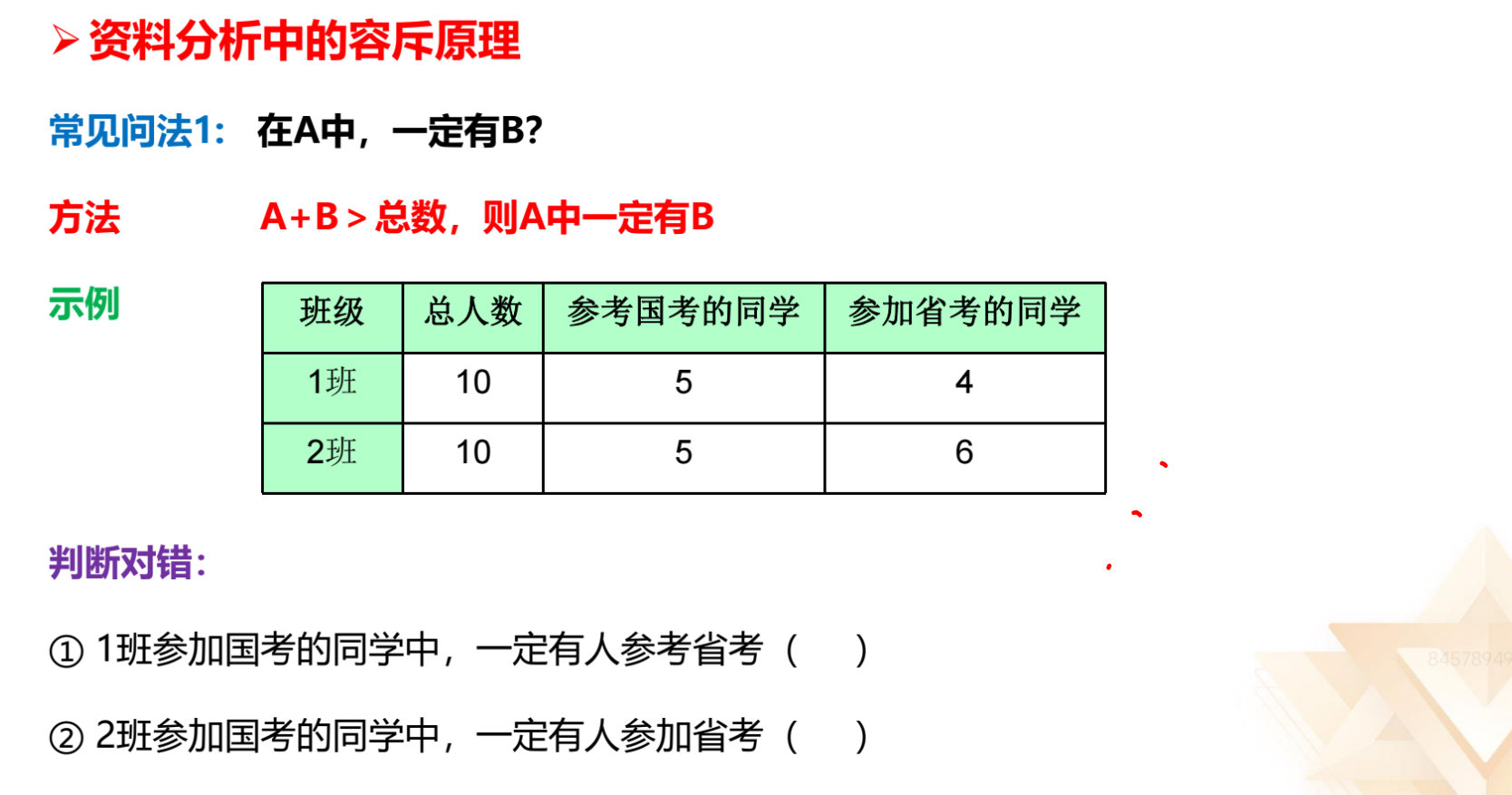
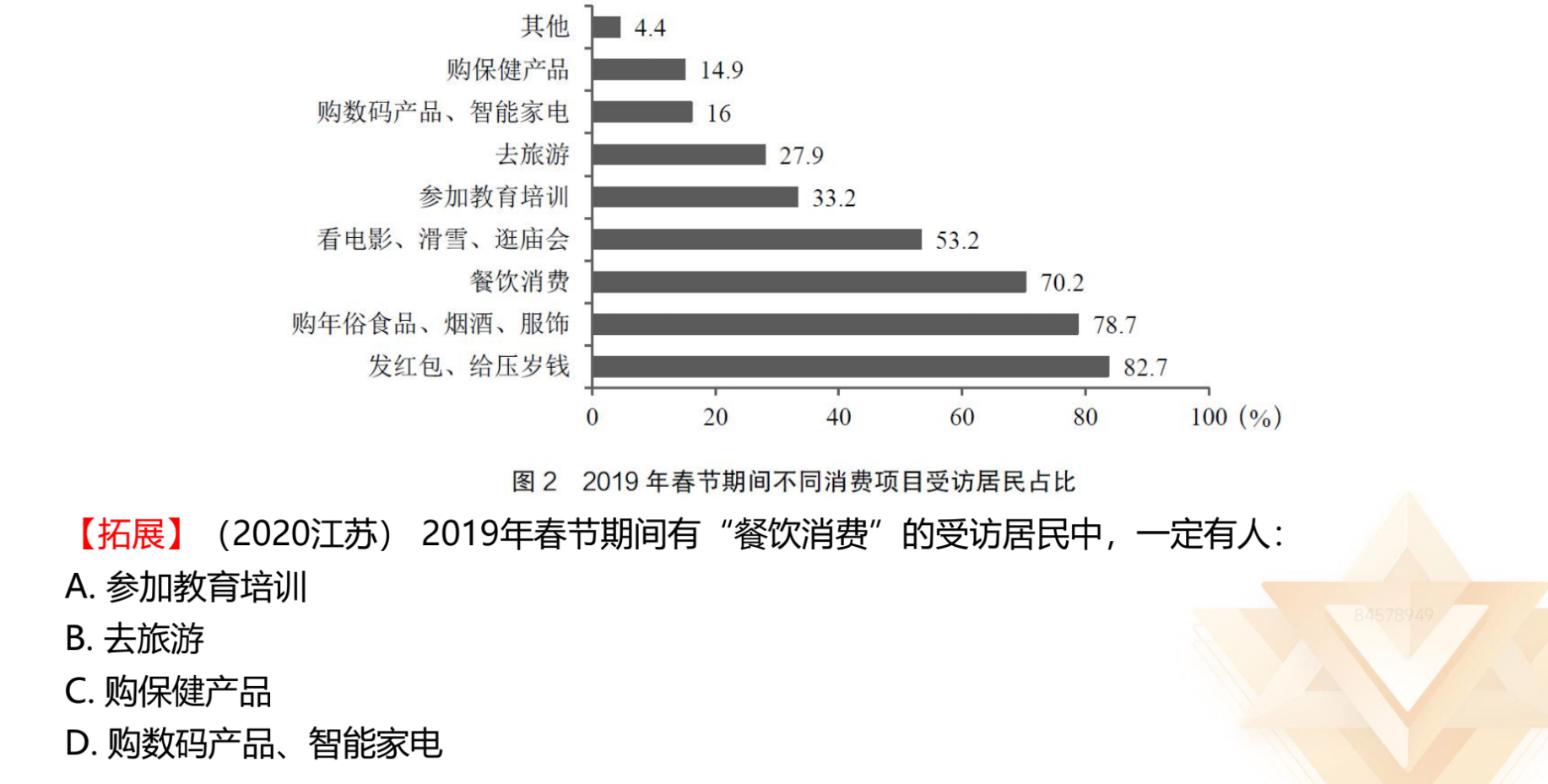
【解析】拓展.有交集，加和超过 100%，33.2%+70.2%＞100%，对应 A 项。
【选 A】

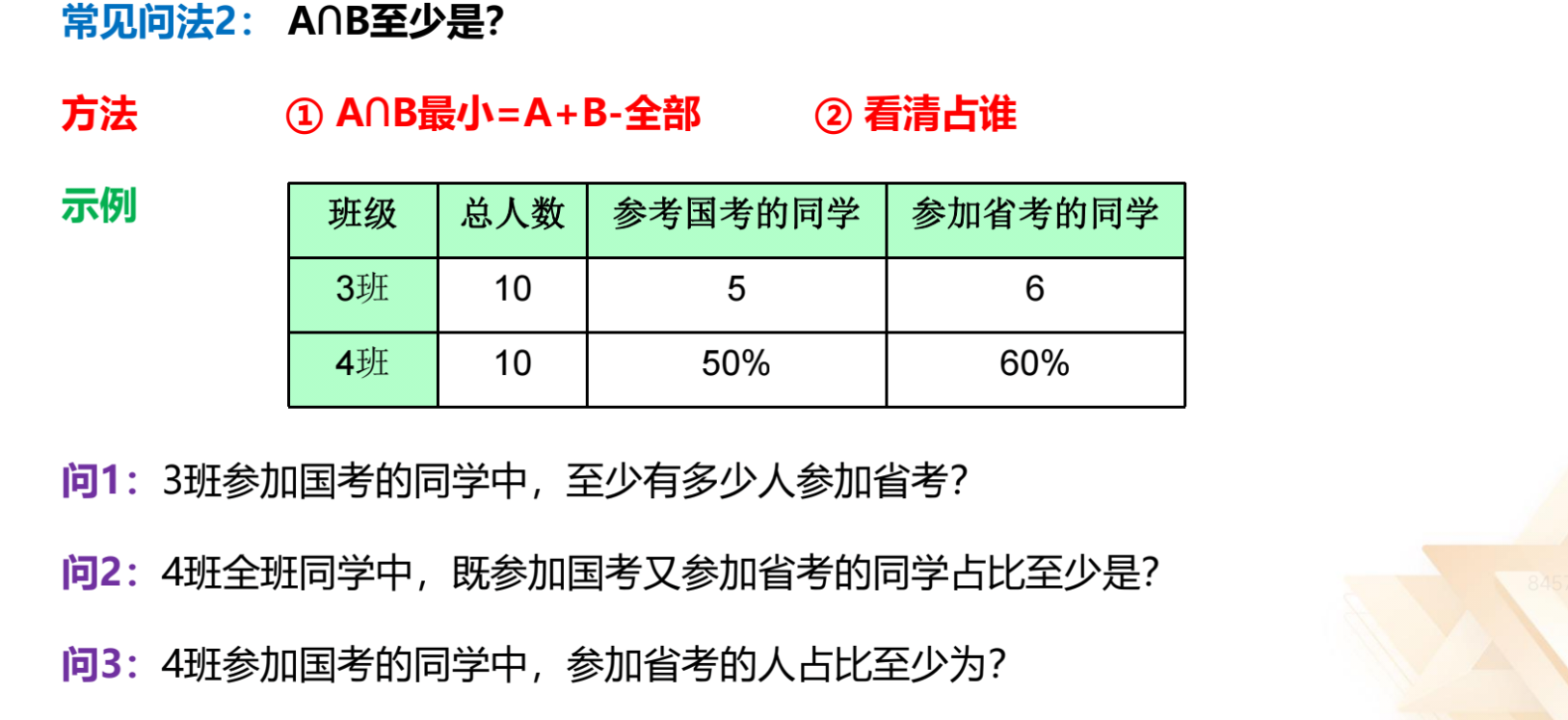
    （1）问 1：3 班参加国考的同学中，至少有多少人参加省考？交集最小是
5+6-10=1，占的是参加国考的人数，至少有 1/5 人参加省考。
    （2）问 2：4 班全班同学中，既参加国考又参加省考的同学占比至少是？交
集最小为 5+6-10=1，占的是全班的人数，占比至少是 1/10。
    （3）问 3：4 班参加国考的同学中，参加省考的人占比至少为？交集最小为
1，参加省考的人占比至少为 1/6。