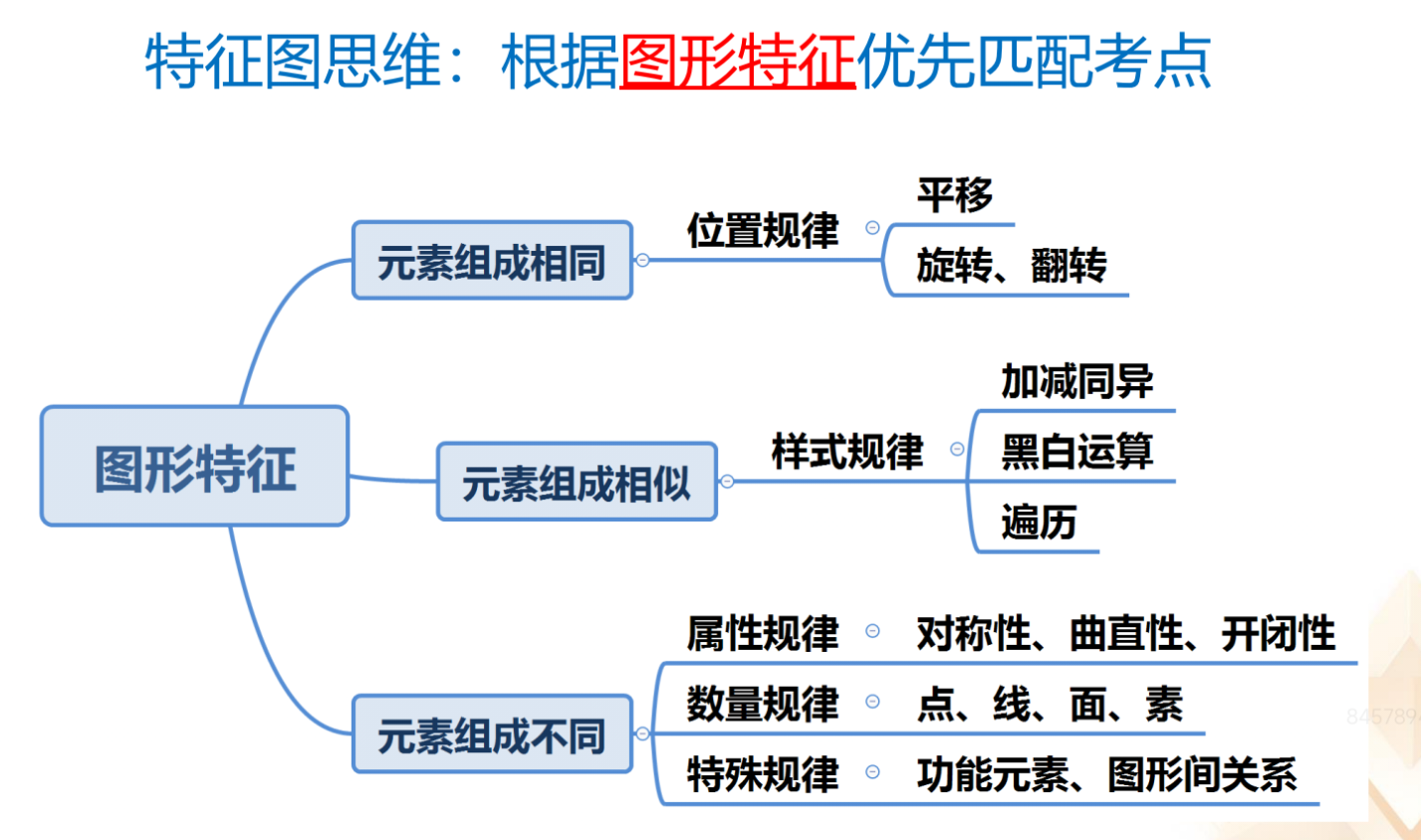
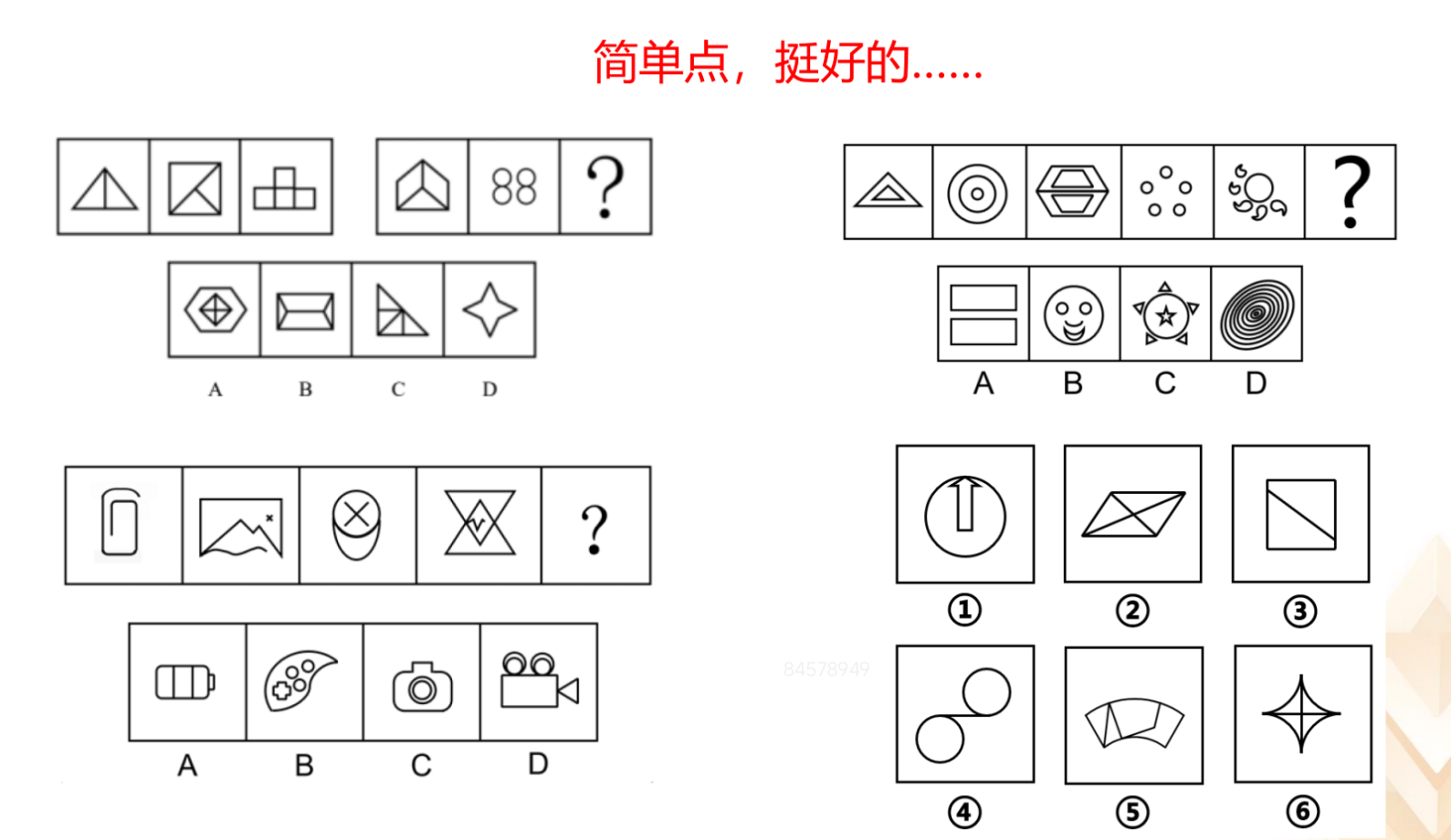
1.要看图形特征。元素组成相同,考虑位置规律;元素组成相似,考虑样式
规律;元素组成不同,先考虑属性规律,其次考虑数量规律,分组分类题常考查
特殊规律。
2.最主要的是知道每个考点的特征图。当题干有黑球、有白球、有空格,数
量相同,元素相同考虑位置规律,结合目前考情大概率考查黑球和空格(空格也
是元素)。当题干有 6 幅图,在转动,考查旋转和翻转的区分。锁定考点之后要
锁定方法,如区分旋转和翻转可以利用时针法;如果每幅图均出现 1 个圆,存在
线与线的相交,优先考虑交点,还有可能考查曲直交点、内外交点,一旦出现曲
线,还会考查切点。

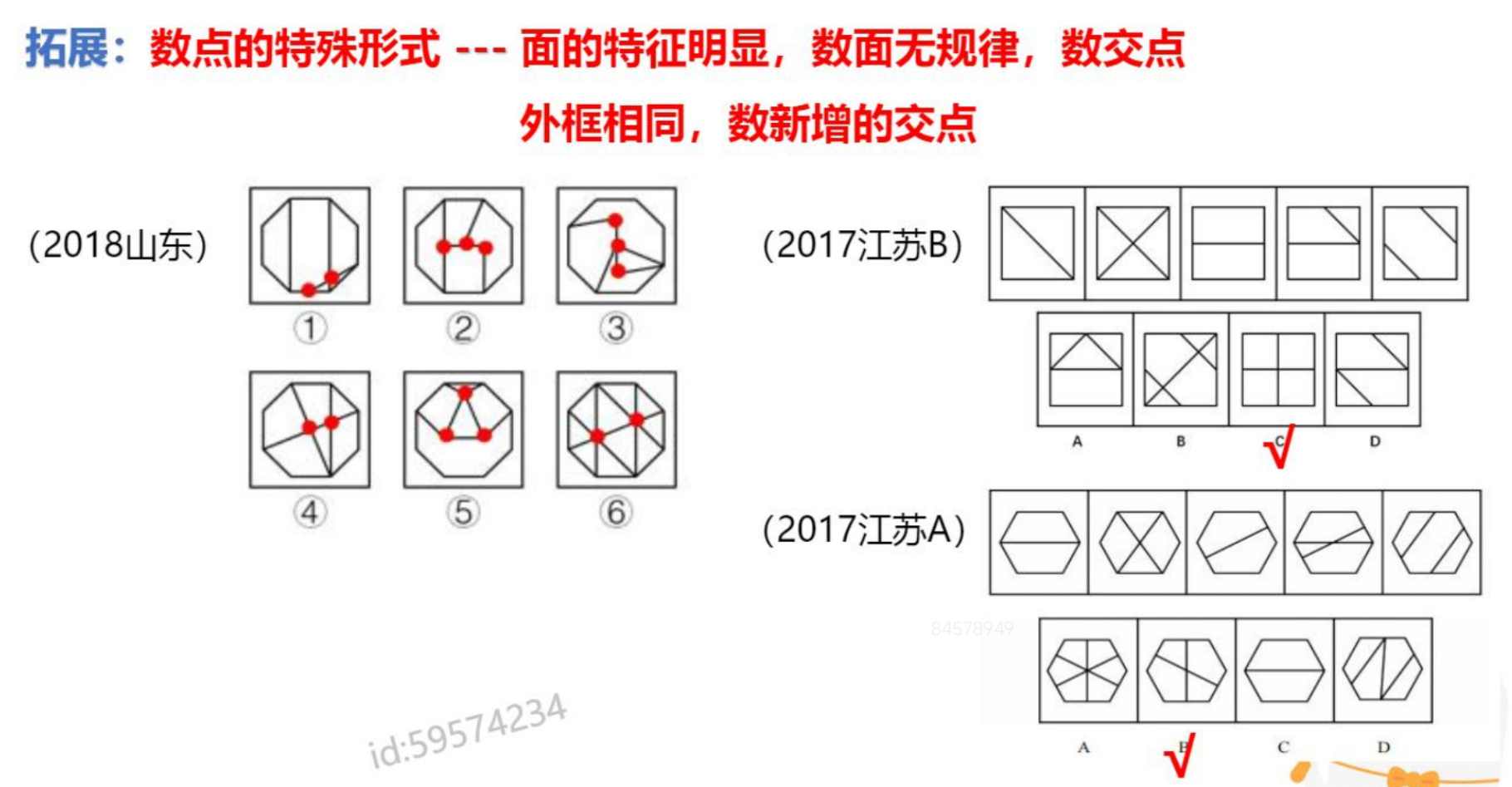
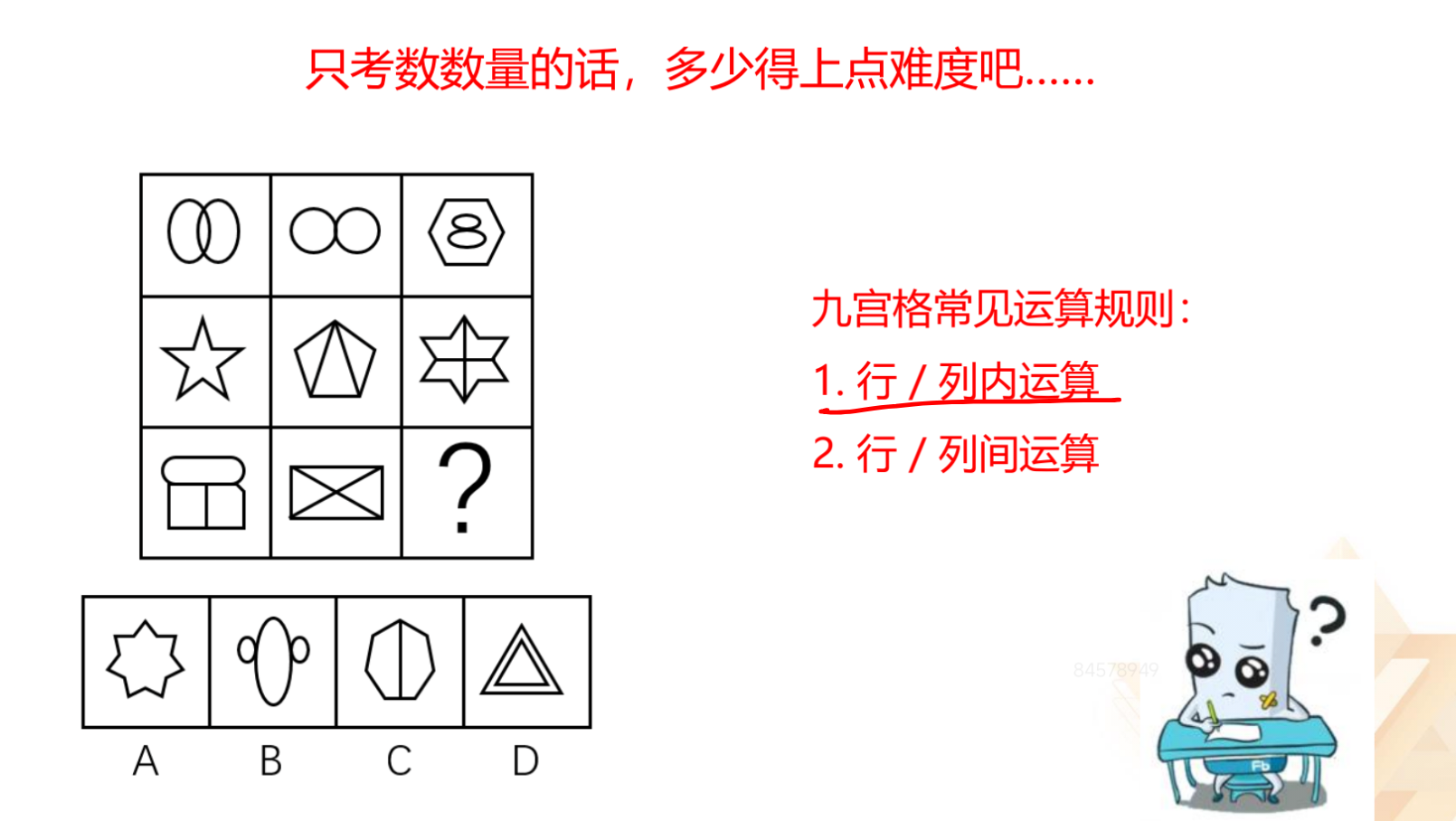
面数量:如讲义的第一题,根据面数量直接分组,但是越简单的题
目越容易想不到。
1.特征:图形被分割、有明显的空白区域。
2.注意:加大难度。
(1)出题形式的变化:如出现汉字、字母、数字。
(2)结合九宫格运算。
1.2019 联考:考虑面数量,第一组图为 2、3、4,第二组图为 3、4,故“?”
图形有 5 个面。
2.2020 联考:题干每幅图面数量分别为 2、3、4、5、6,故“?”处图形面
数量为 7。
3.2021 联考:题干每幅图面数量分别为 0、1、2、3,故“?”处图形面数
量为 4。
4.不是所有题目都很难,存在简单题和送分题。
1.如上图,出现空白区域,考虑数面,第一行分别为 3、2、3,第二行分别
为 1、3、4,第三行分别为 3、4,横行相加均为 8,故“?”处面数量为 1,对
应 A 项。
2.九宫格常见运算规则:
(1)行/列内运算,如第二行为 1+3=4。
(1)行/列间运算:每一行相加是同一个数。
(3)国考考查的概率相对较小,因为国考已经连续 3 年只有 3 道九宫格的
题目,均考查样式类规律(一年是求同求异,两年是黑白运算)
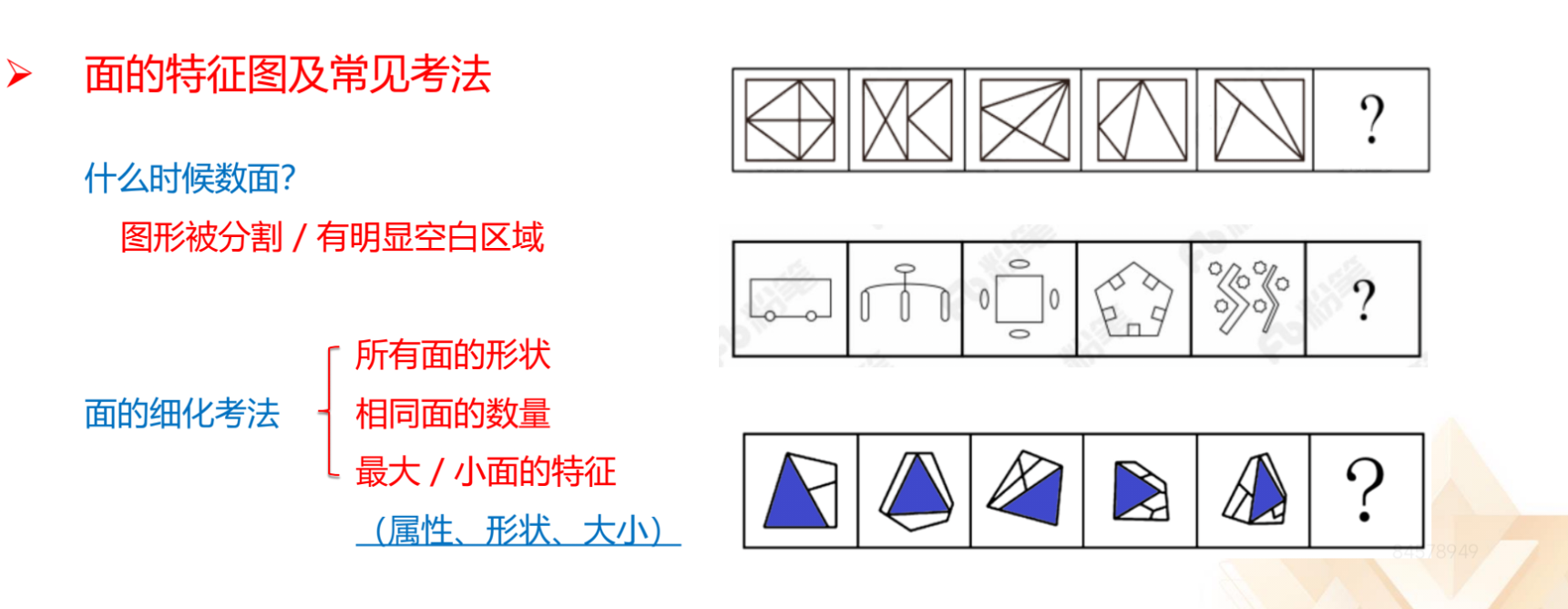
【注意】面数量细化考法:图形存在数面特征,但是数面无唯一答案,考虑
面的细化。
1.所有面的形状:三角形、四边形、五边形。如图一,题干每幅图面数量分
别为 8、7、6、5、4,且每个面都是三角形。
2.相同面:如图二,不能考虑所有面的形状,考虑相同面的数量,图 1 有 2
个相同面。
3.最大、最小面:某个图形存在最大/最小面,考查形状/属性/大小,其中
大小考查较少,属性主要考查对称。遇到一道题,如果数面无规律,观察任意一
幅图中是否有所有面的形状的规律,是否存在相同面、最大/最小面。
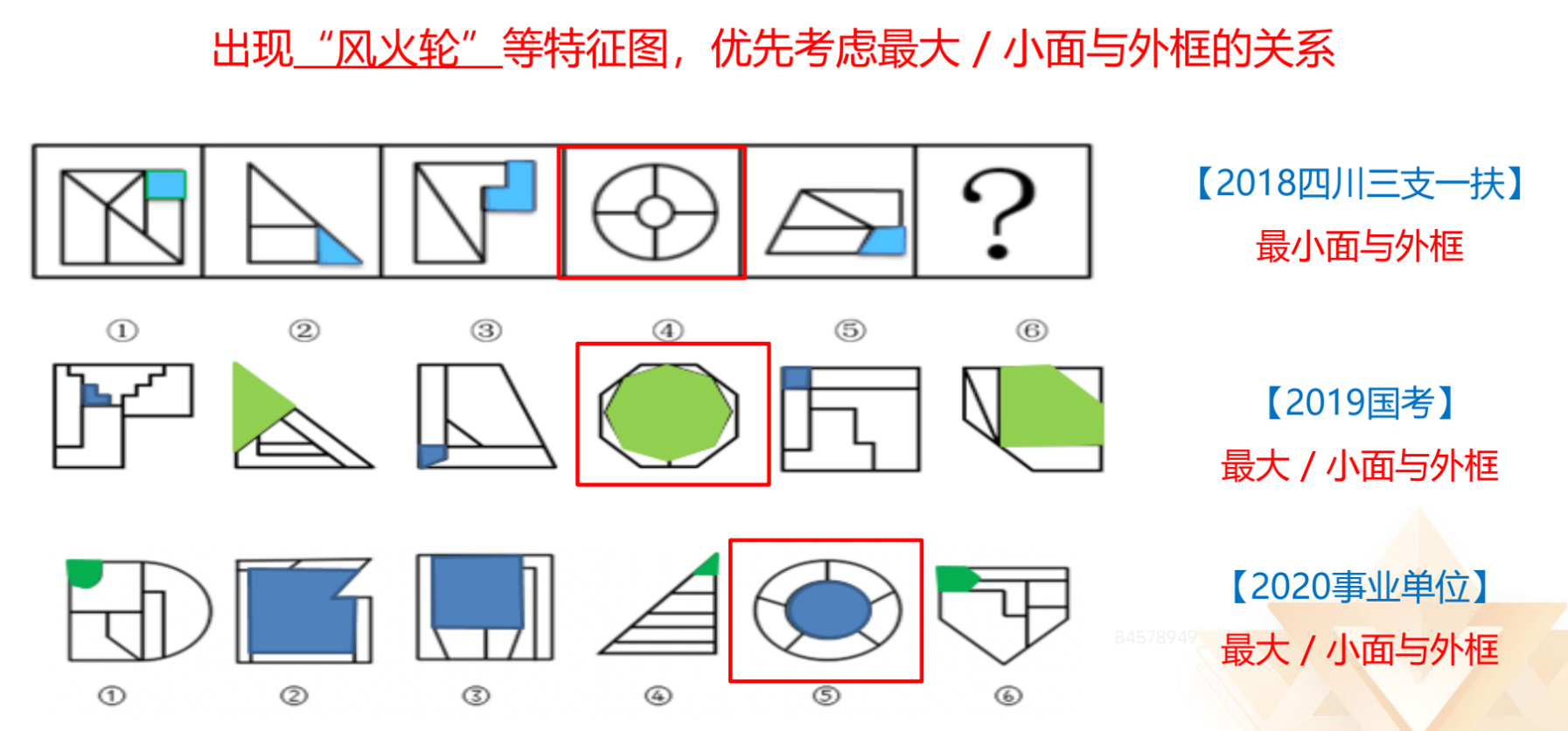
出现“风火轮”,考虑最大/小面与外框的关系。
1.上图中红框圈出的图形均为“风火轮”图形。
2.2018 四川:考查最小面和外框相似。
3.2019 国家和 2020 事业单位:最大面与外框相似为一组,最小面与外框相
似为一组。
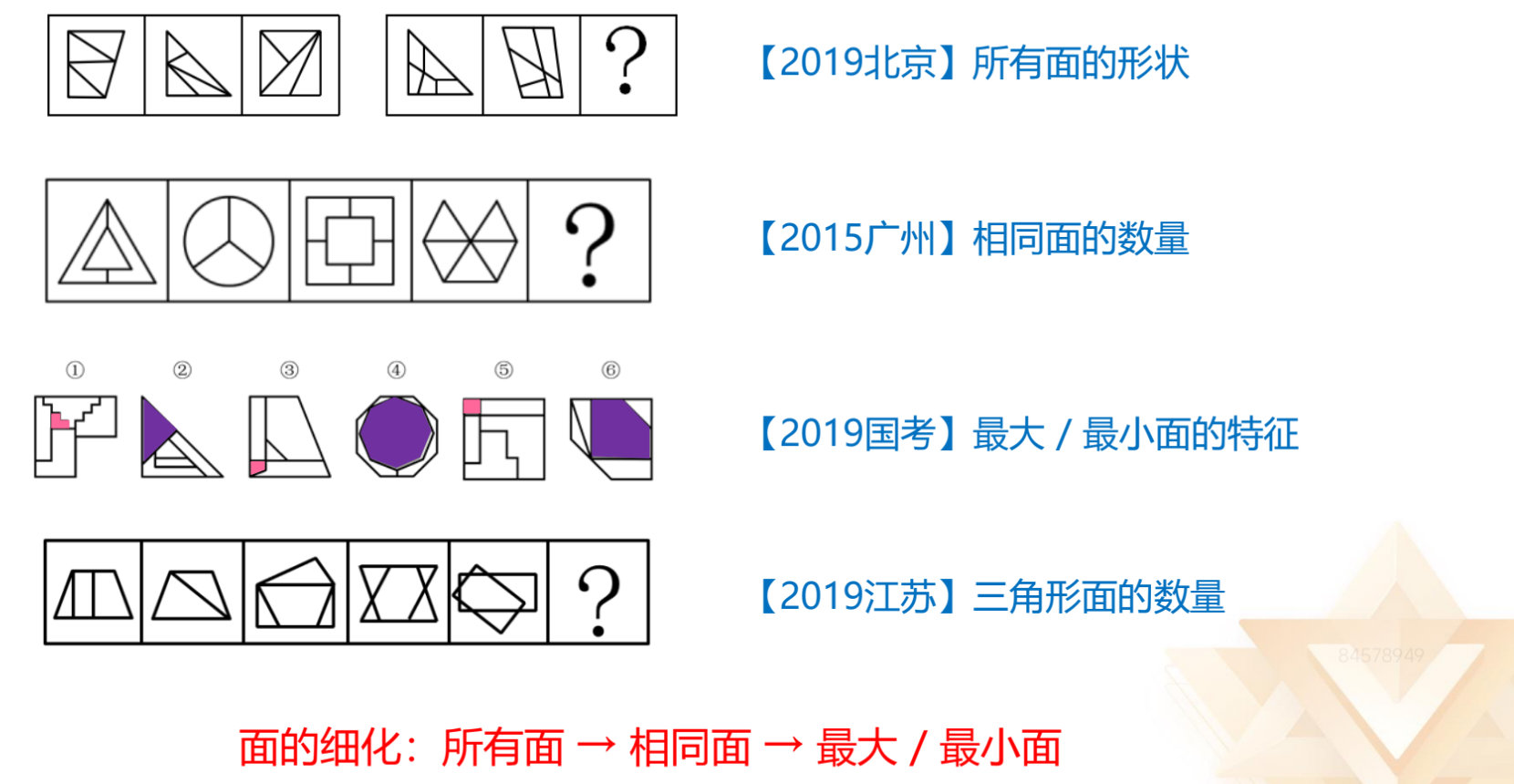
面的细化:所有面→相同面→最大/最小面。
1.2019 北京:第一组图所有面都是三角形,第二组图所有面都是四边形。
2.2015 广州:题干每幅图相同面的数量分别为 1、2、3、4、5,故“?”处
有 6 个相同面。
3.2019 国考:观察最大/最小面的特征。
4.2019 江苏:每幅图均存在多个三角形,考虑只数三角形面的数量,每幅图
分别为 1、2、3、4、5,故“?”处有 6 个三角形面。
总结:出现典型数面特征,但无规律,考虑面的细化考法。
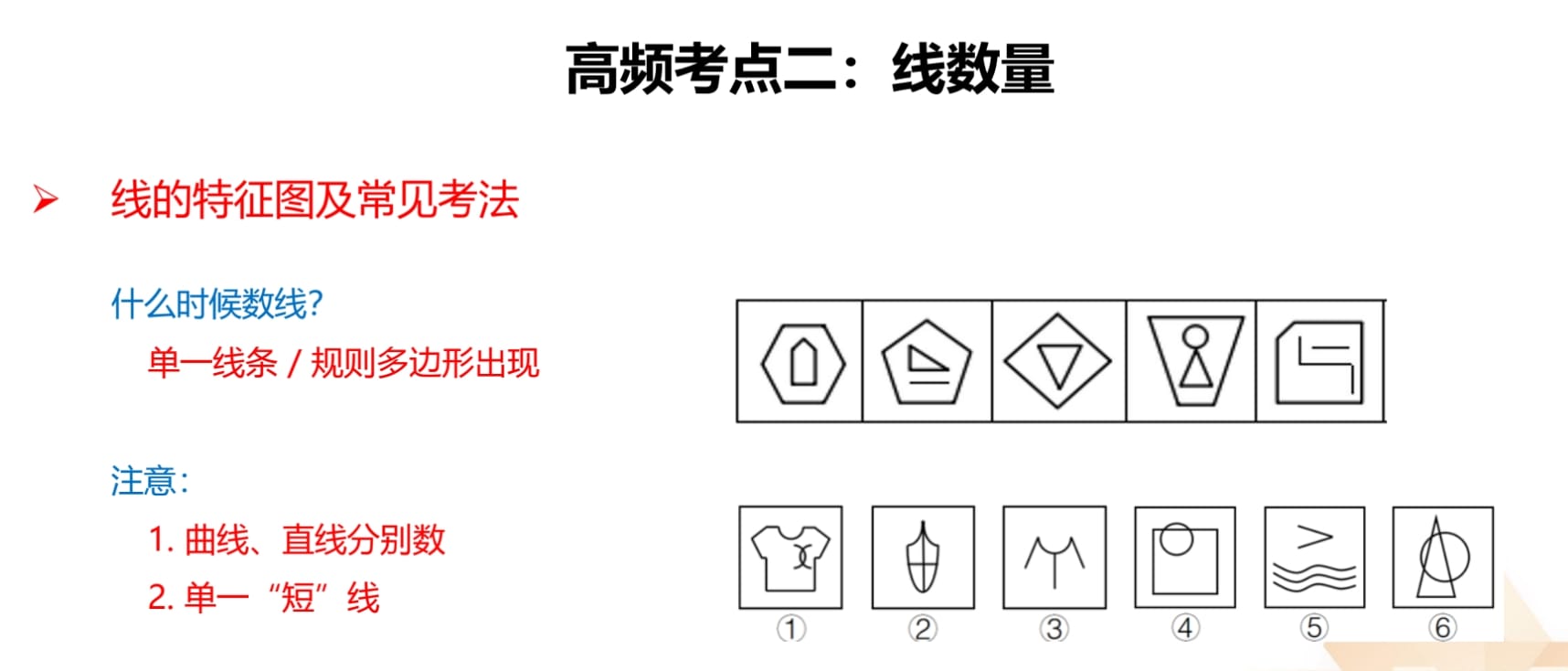
线数量:面数量很简单,而线数量很容易想不到。
1.特征图:单一线条、规则多边形(外框是三角形、四边形、五边形等,还
有可能要看外框有几条线)。
2.注意:
(1)曲线和直线要分开数。
(2)单一“短”线:单一线条不一定是长直线,还有可能是单一“短”线。
3.如图一和图二,均出现单一线条。如图一,图 4 有 7 条直线,1 条曲线,
曲线和直线要分开数。

1.内外分开数:每幅图出现外框。
2.横竖分开数:出现横线和竖线。
3.曲直分开数:每幅图均出现曲线,考虑曲线数和曲直分开数。
4.先分开数,若无规律,再考虑做运算(加减乘除)。

所有图形均有曲线——曲直性、曲直交点、曲线数相关。如图二,
题干出现曲线和单一线条,考虑数线。
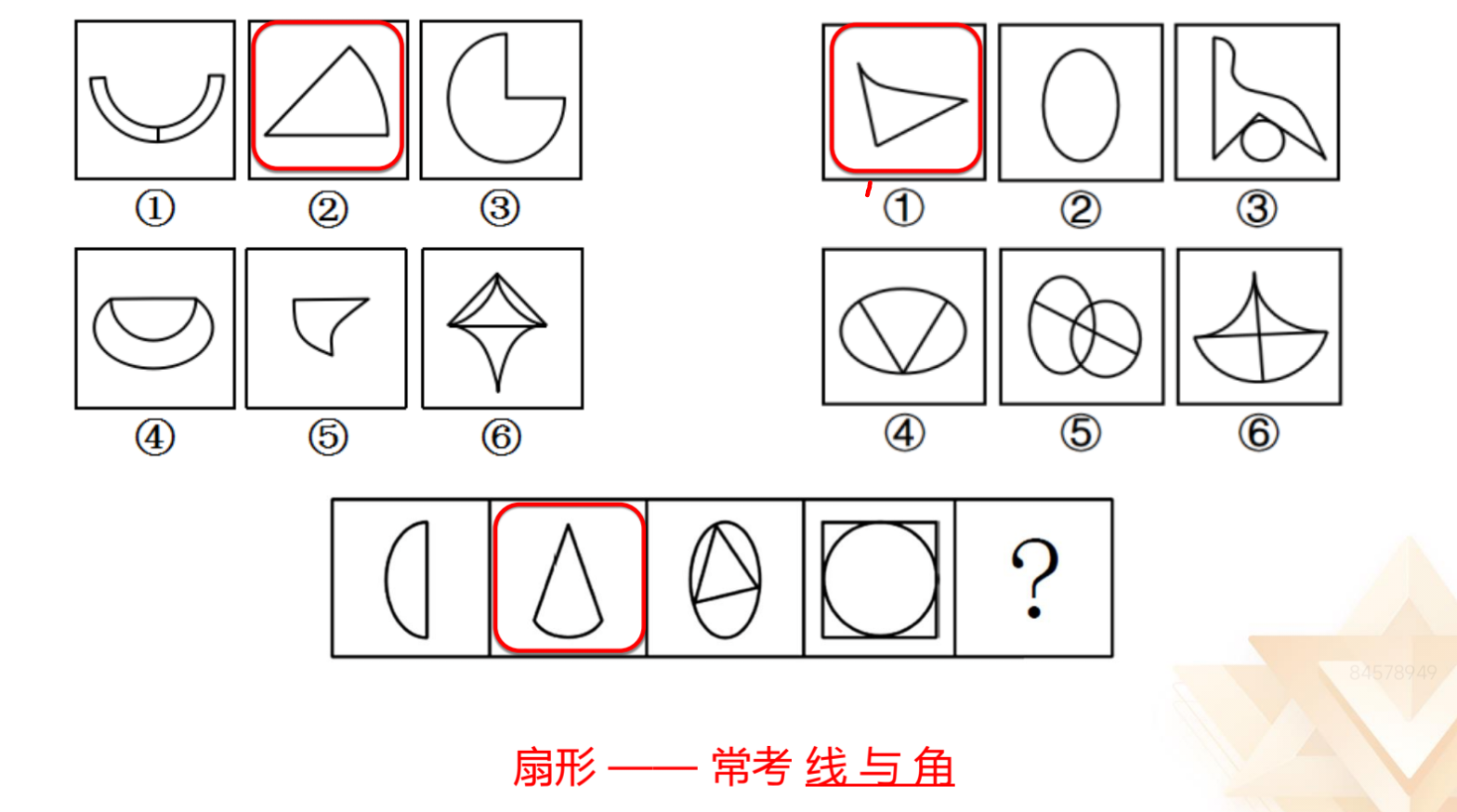
如图三,框出的图形均出现扇形及其变形图,优先考虑线(直线与
曲线分开数)与角(扇形只有 1 个角)。

如上图,图形明显分内外,考虑内外分开看,如果不行可以就做运
算(加减乘除)。
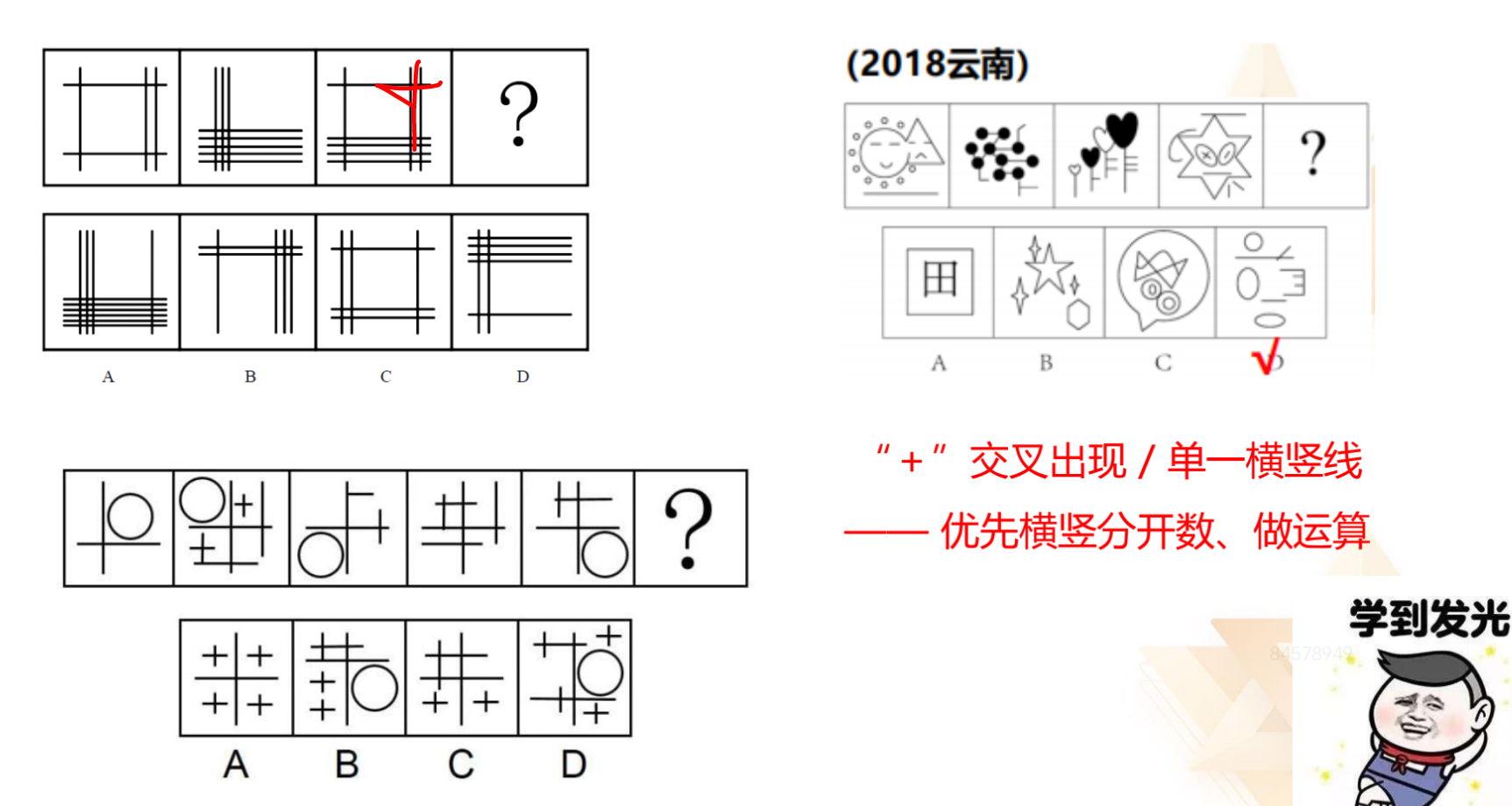
1.如上图,“+”交叉出现,2018 云南的图 1 出现很多单一线条,且出现多
个横线和竖线,优先考虑横竖分开数,其次考虑做运算。
2.曲直分开数考查较多,横竖分开数考查较少
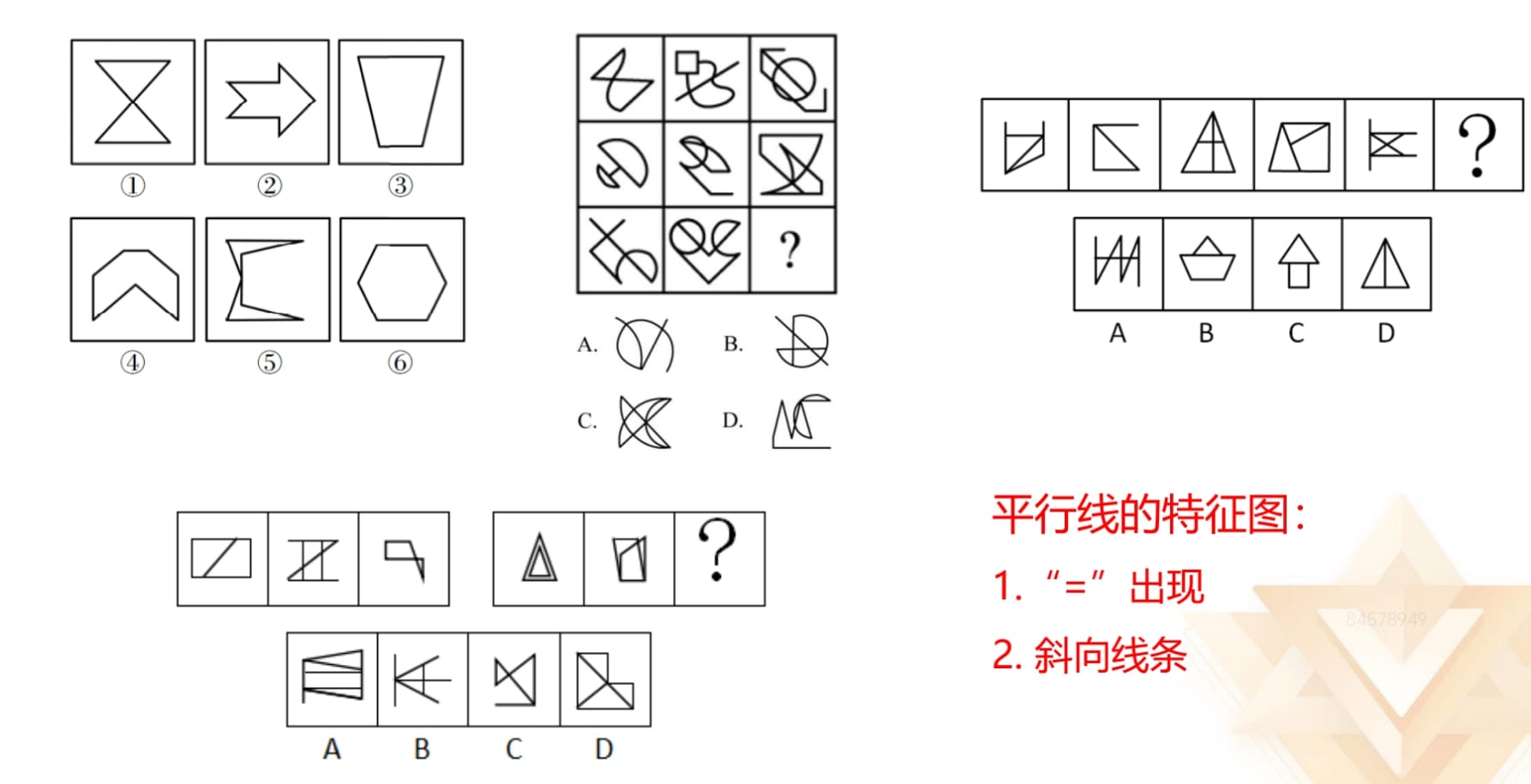
平行线的特征图:
1.“=”出现。
2.斜向线条。

笔画数:属于高频考点,2020 年国考就考查过,联考几乎每年都考
查。
1.一笔画:优先考虑笔画数,不要“走投无路”才考虑笔画数。
(1)连通图:如图 1,是连通图,图 2 是非连通图,多部分图形分开数并相
加。
(2)奇点数=0 或 2。一个点引出奇数条线是奇点,一个点引出偶数条线是
偶点。
2.笔画:笔画数=奇点数÷2;多部分图形分别数。如果 1 个点发射出 7 条
线,7 是奇数,是奇点。很多同学将奇点的概念认为是引出 3 条线。
3.注意:
(1)所有的端点都是奇点。
(2)图形的奇点数一定是偶数个,如果数出奇数个奇点,说明数错了。
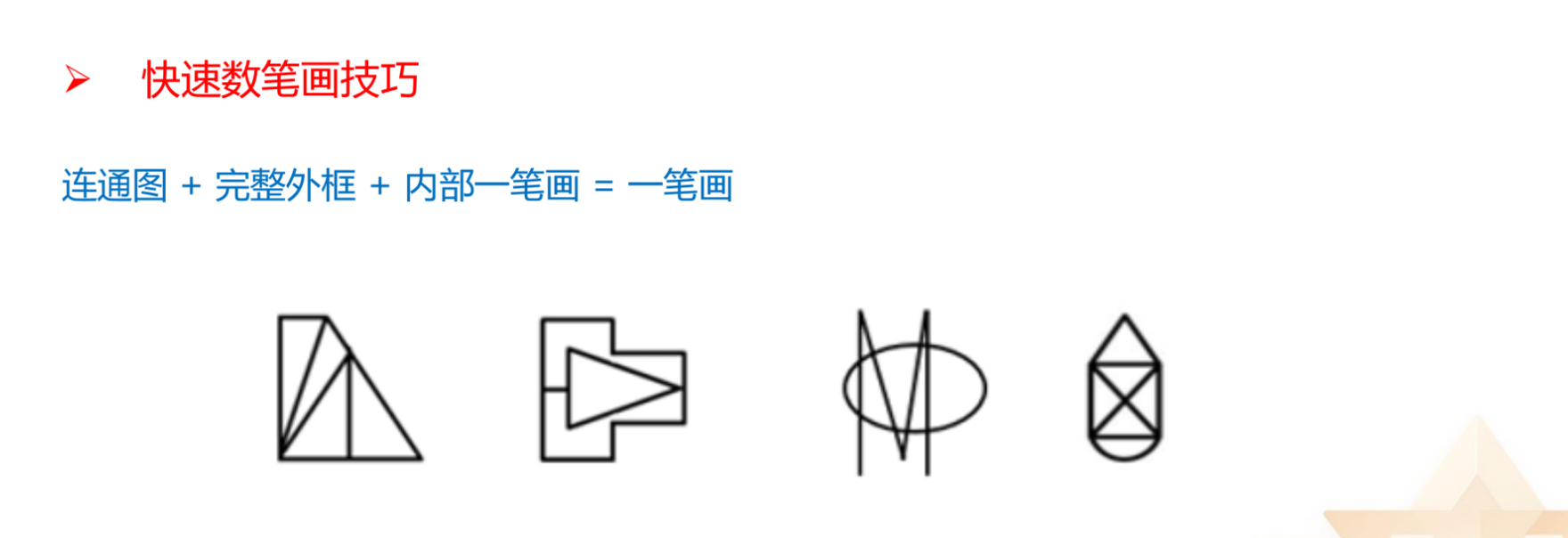
快速数笔画技巧:
1.连通图+完整外框+一笔画图形=一笔画。
2.如上图,如果将外框去掉,内部明显可以一笔画成,故整体是一笔画图形。

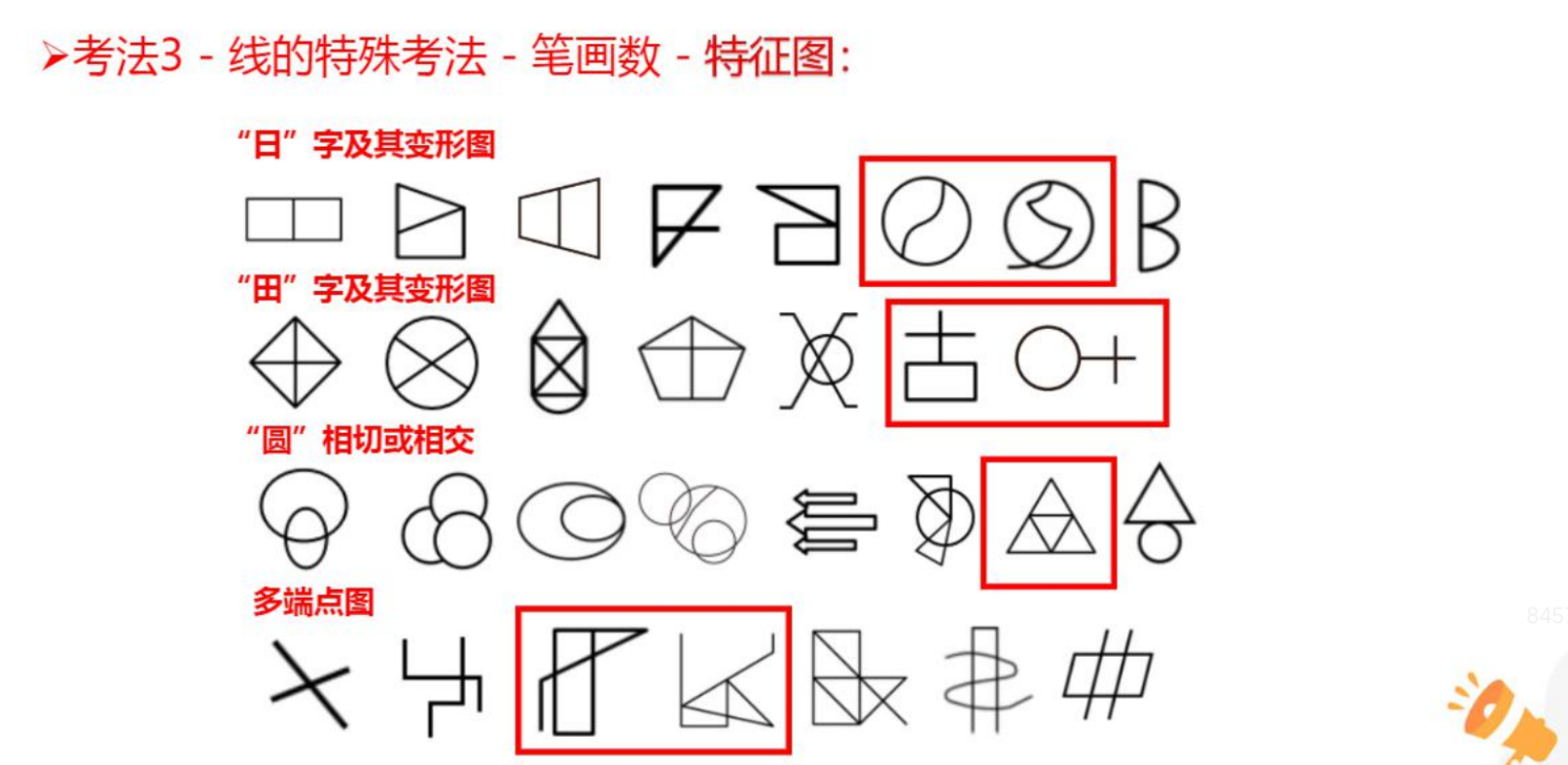
笔画数特征图:
1.“田”字变形图、“日”字变形图、“古”字变形图、A、B、H。
2.“圆”相切或相交:建议记忆为图形相交,可能会出现变形,如将圆都变
为方形。

1.多端点(考查端点都是奇点):如第一行图,除了是多端点,还存在明显
的线与线相交,有交点的特征。建议数简单的考点,考场上如果前面的题目考查
过笔画数,建议考虑数交点。
2.“一线牵”(考查连通图考虑笔画数):如第二行图,几个面用线条连在一
起。

黑白块的常见考法:
1.平移:黑块个数相同。
2.黑白运算:黑块个数不相同,且为九宫格、两组图。
3.出现“等腰”、“S、N、Z”:看对称(整体、局部)。如果平移和黑白运算
均无规律,优先考虑对称,因为不用数数。对称:
(1)可以看黑块。
(2)可以看白块。
(3)可以看轴对称、中心对称。
4.黑白块分堆儿,乱,考虑数黑/白部分,先分开、再运算。
5.黑白块相连:优先看笔画,还可以看白块部分。
6.一组图+黑球非常多、散,考虑相邻比较。如图一,相邻两幅图只有一行
发生变化,其他行都一样。
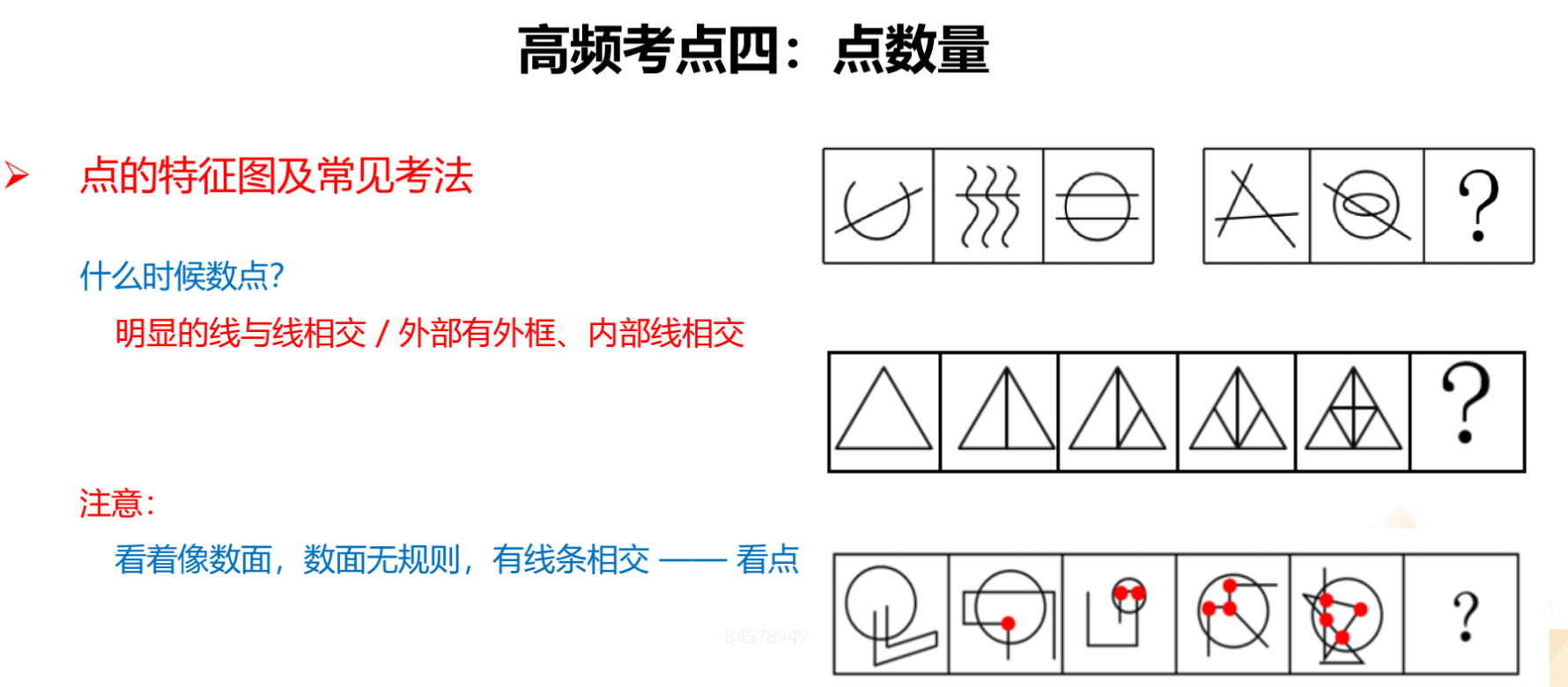
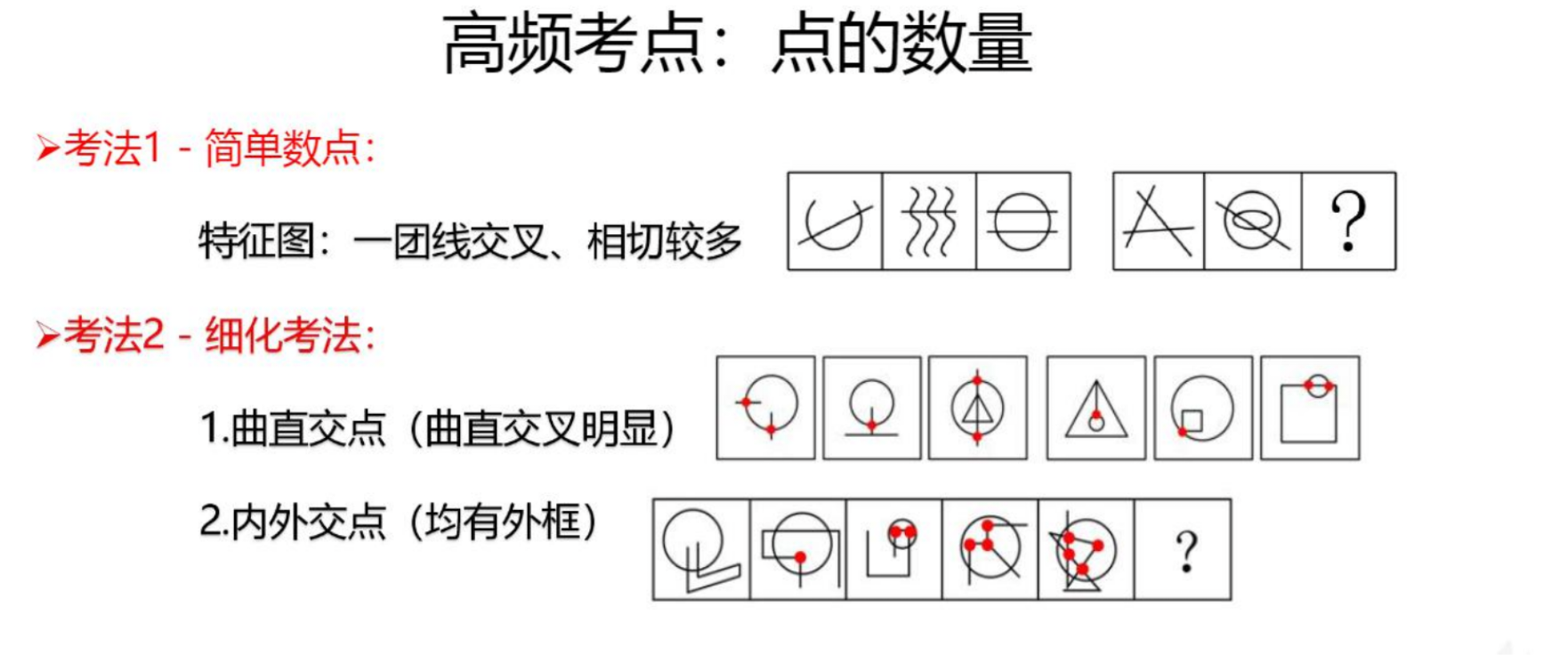
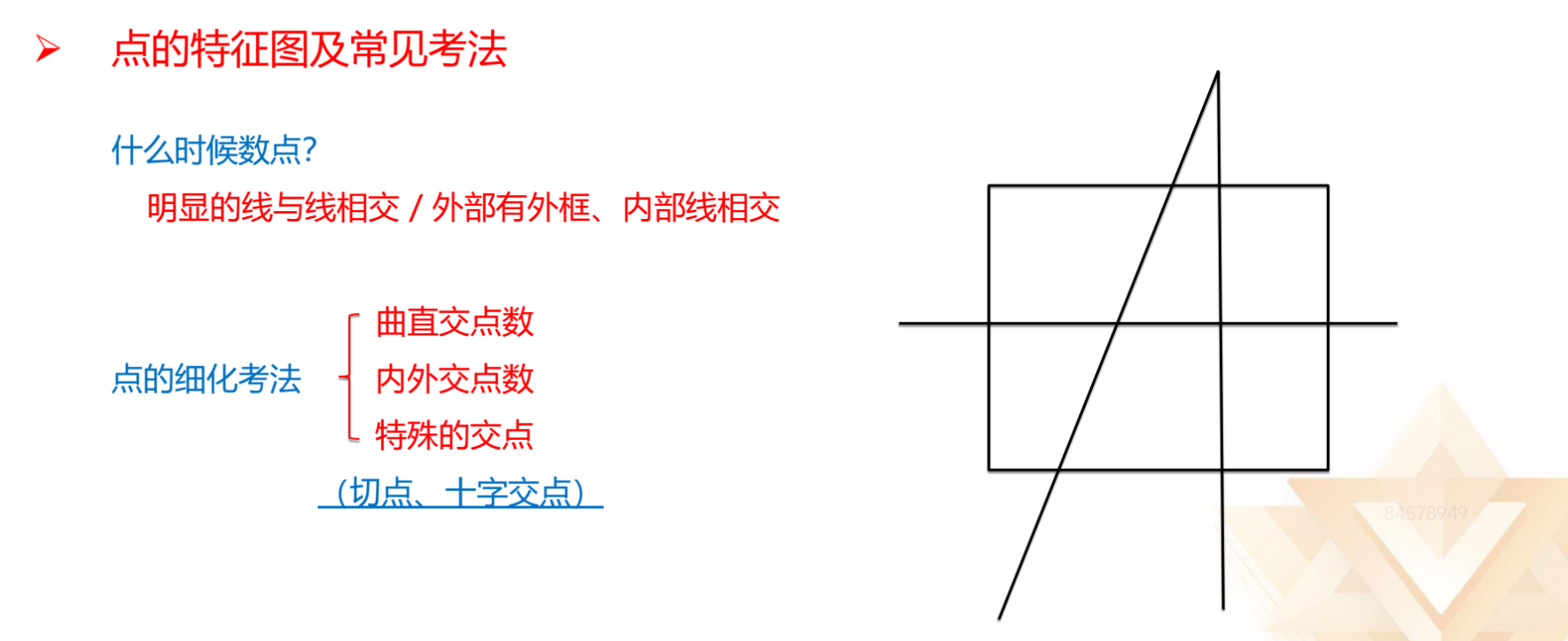
点数量:数的是交点。
1.什么时候数点:
(1)明显的线与线相交。
(2)外部有外框,内部明显存在线相交。
2.看着像数面,但数面无规则,往往符合“外部有外框,内部线相交”的特
征,可以数交点。
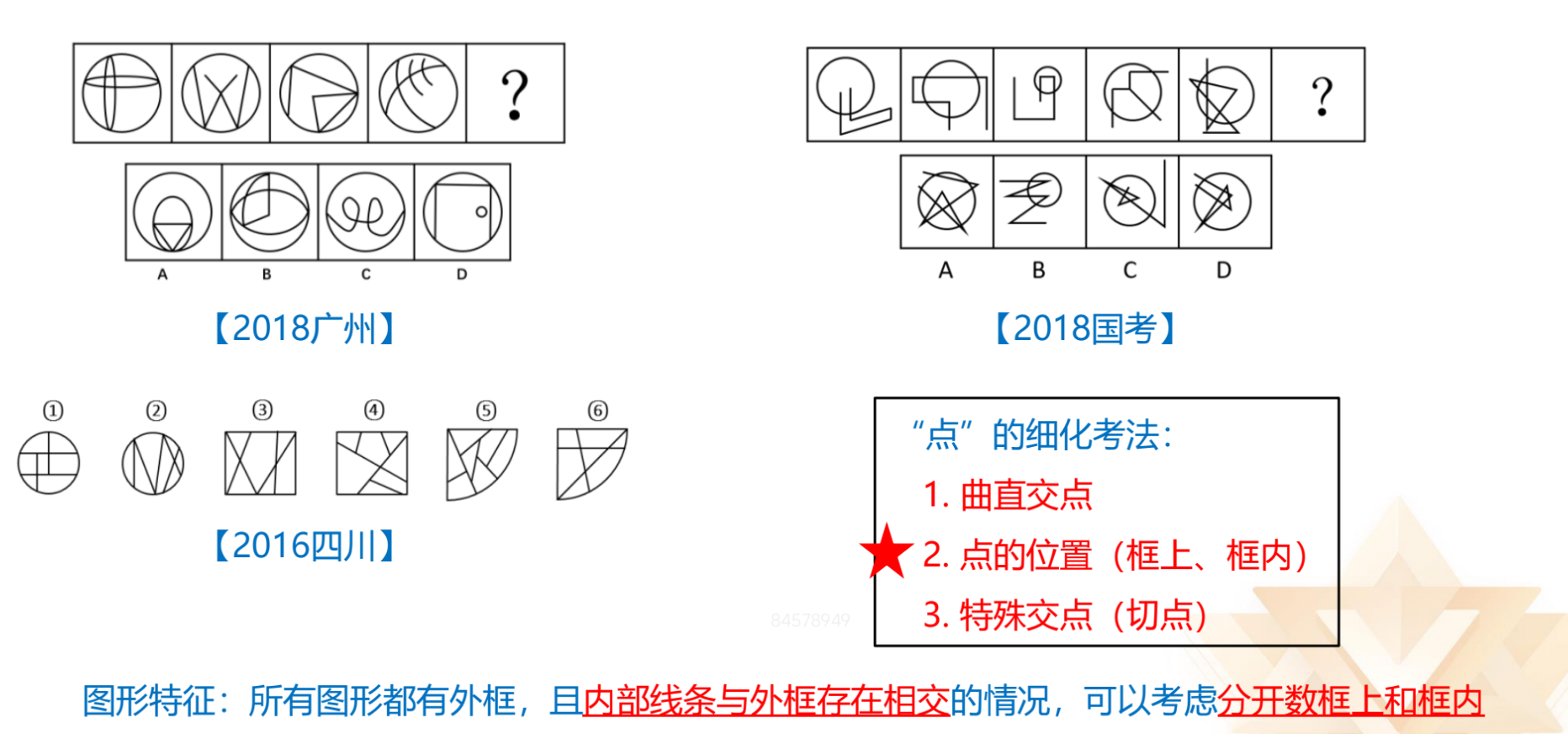
点的细化考法:
1.曲直交点数,所有图形存在线与线相交的位置关系,且有曲有直。
2.内外交点数,每个图形都有外框,且存在相交的位置关系。如上图,“内
外交点”的说法不准确,交点其实有三类,第一类封闭空间内部交点数为 2,第
二类封闭空间外部交点数为 1,第三类线条与外框之间的交点数为 6(现在考试
考查较多的是内部线条与外框的交点,外框本身自带的交点可以先不数,如果数
上有答案,不数没有答案时,再考虑)。
3.特殊的交点:
(1)部分图形相切,可能考虑笔画数,也可能考查交点;如果所有图形都
相切,则大概率考查交点,且很有可能考查特殊交点中的切点。
(2)“十”字交点,目前公务员考试中没有考查过,事业单位考试有所考查,
将交点分为普通“十”字交点与特殊的顶点,顶点是两条先相交不出头,而普通
点的细化考法的“十”字交点两条线相交后会出头。
4.关于点的细化不仅仅要知道曲直交点和内外交点,还要知道特殊交点(切
点、“十”字交点)。现在的考试中,相切考查较多,无论是山东、江苏、国考等
都有考查,而山东、江苏、国考是比较常见创新出题的考试,如果考试效果不错,
很有可能在其他省份推广。
点的细化考法:
1.曲直交点。
2.点的位置(框上、框内),难度更大。
3.特殊交点,公务员考试主要考查的是切点,事业单位主要考查的是“十”
字交点

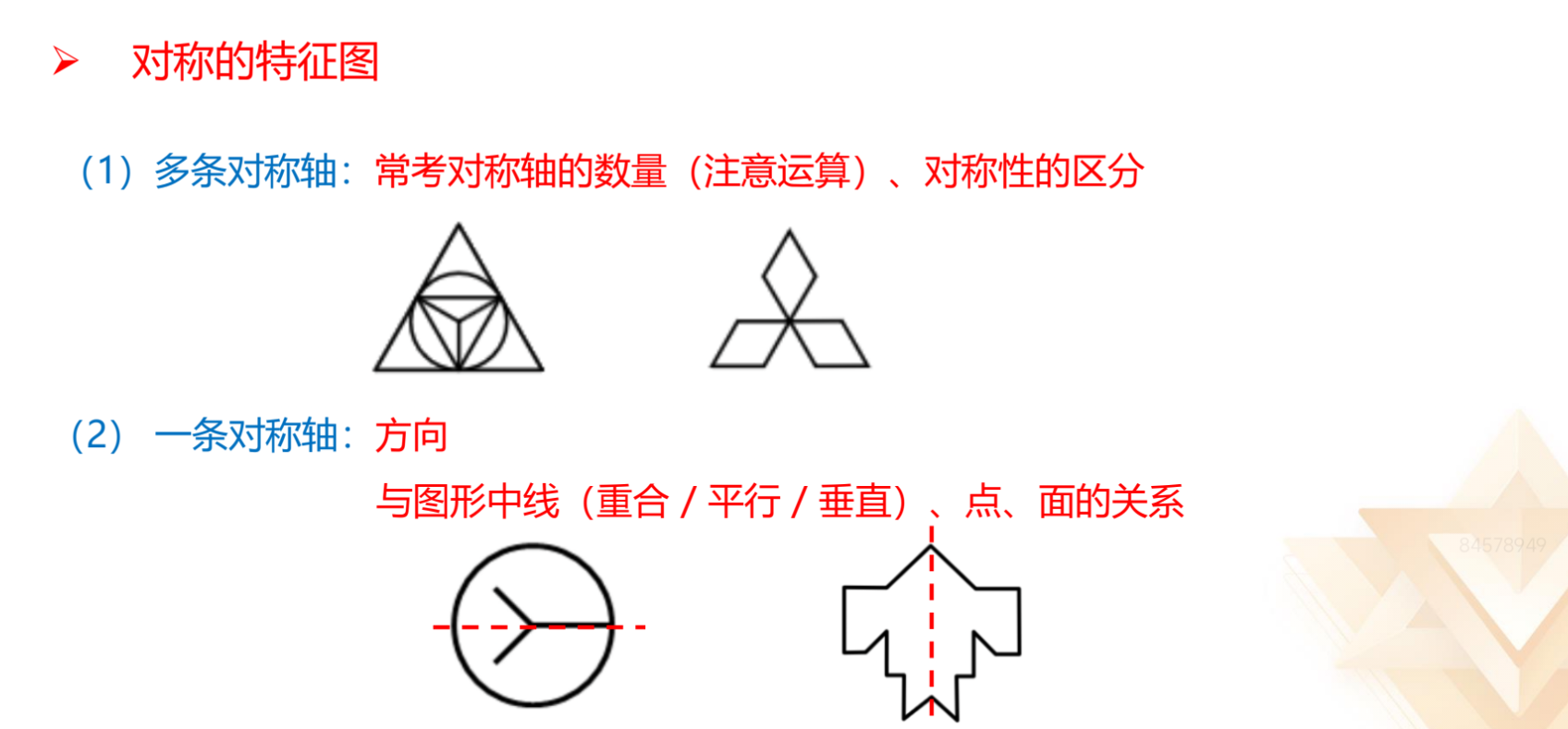
对称性:
1.轴对称:“等腰”元素出现、斜向箭头。
2.中心对称:平行四边形、“S、Z、N”及变形、“大风车”及两个相同图形
反着放。
3.轴+中心对称:包含两条相互垂直的对称轴。
做题时,可能一眼能够识别出考查对称性,但问题是不知道考查的
是什么,选不出答案。识别出考查对称性时,要优先画出对称,因为考法大概率
与对称轴相关。
1.多条对称轴:
(1)对称轴的数量关系,可以考运算。
(2)对称性的区分,有 2、4、6 条等偶数条对称轴的图形基本都是轴+中心
对称,奇数条对称轴一般是轴对称。
2.一条对称轴:
(1)方向,看方向如何旋转。
(2)对称轴与图形中线、点、面之间的位置关系,如第二行例图,图 1 对
称轴与图形的 1 条线重合,图 2 对称轴经过图形的 2 个点、1 个面。
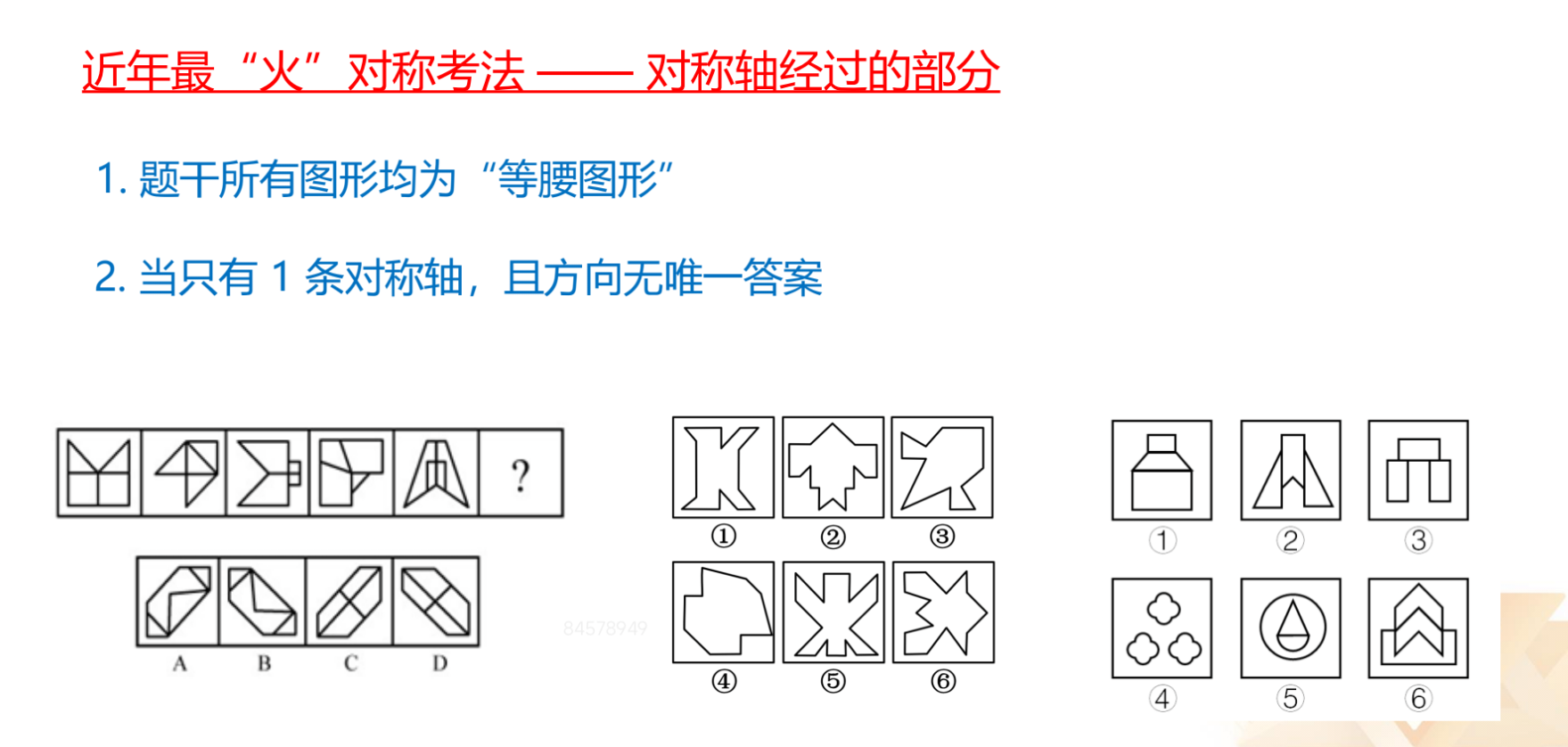
对称轴经过的部分:
1.图形特征:
(1)题干所有图形均为等腰图形。
(2)当只有 1 条对称轴,且方向无唯一答案。
2.图一:考查对称轴与图形中的线重合还是垂直。
3.图二:考查对称轴经过 2 条垂直线还是 2 个交点。
4.图三:考查对称轴经过 3 个面还是 1 个面。
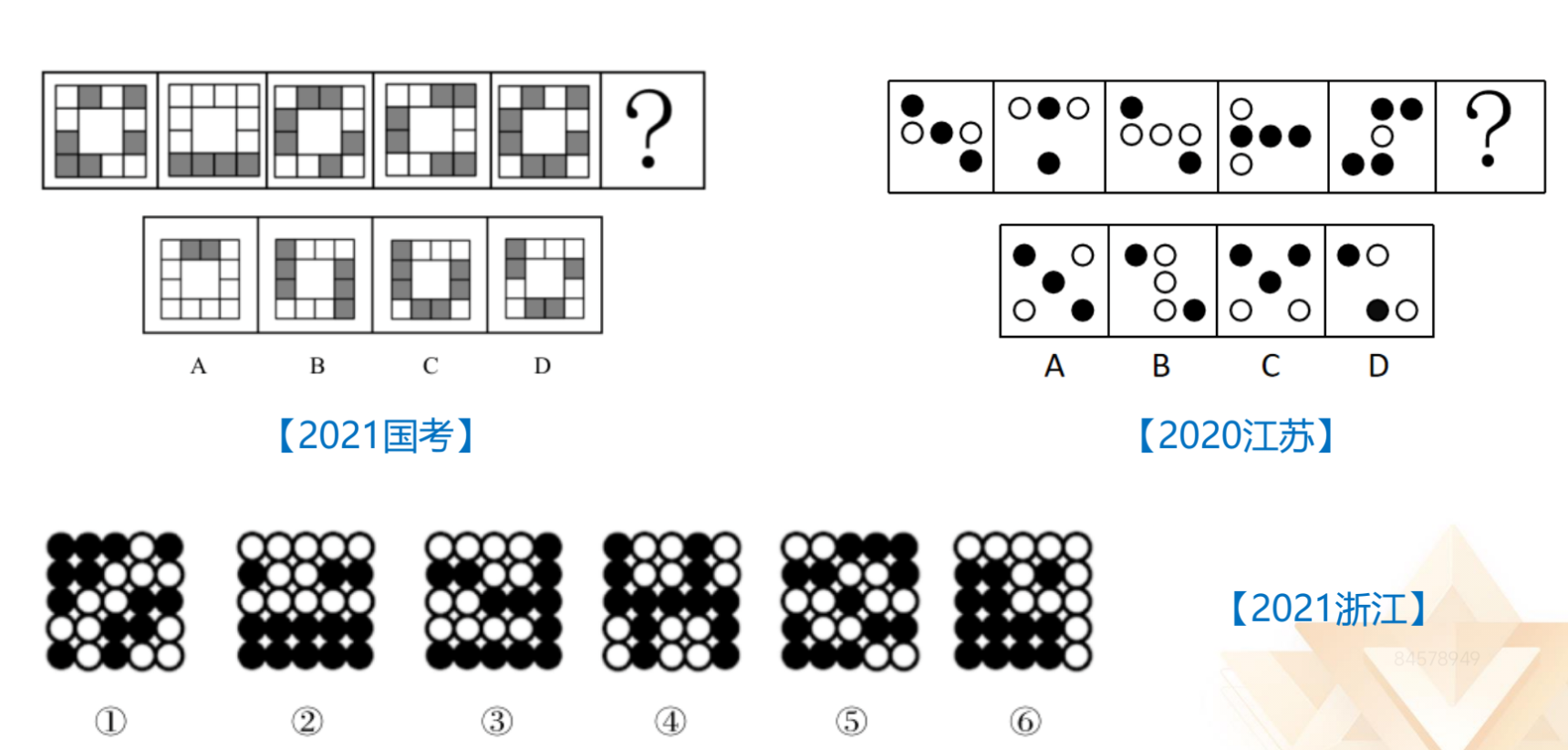
1.2021 国考:黑白块直接看对称。
2.2021 浙江:图①黑球轴对称;图②白球轴对称;图③白球中心对称;图④
白球中心对称;可以看白球的中心对称与轴对称,图⑥白球轴对称。图①黑、白
球均为轴对称,可以只看白球。
3.黑白球考查对称性是现在非常常见的考法,黑、白均可以看,也可以结合
在一起看;可以看中心对称、轴对称、轴+中心对称。
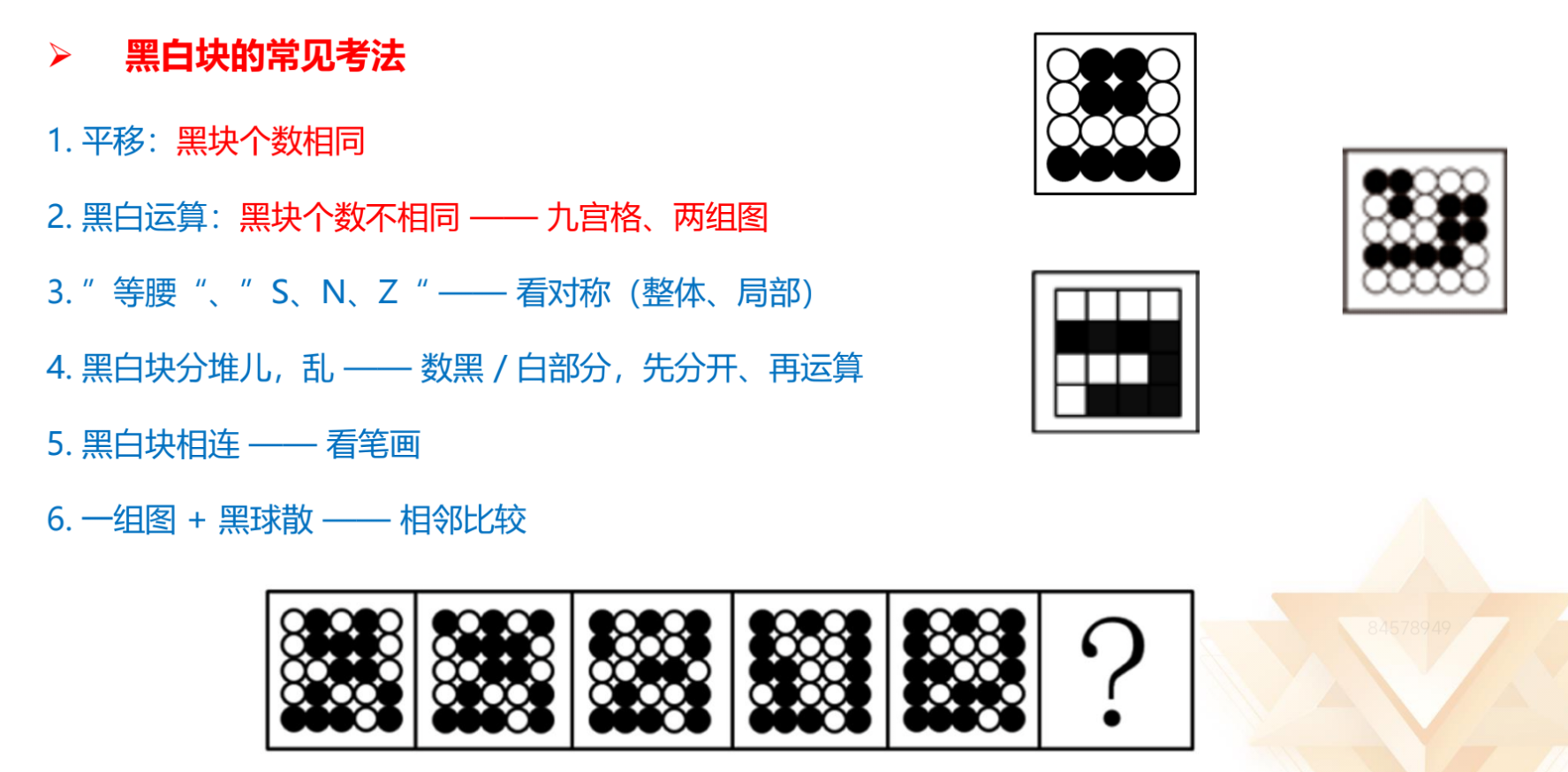
黑白块的常见考法:前面已经进行了总结,一定要记住,现在的考
试中非常常见。
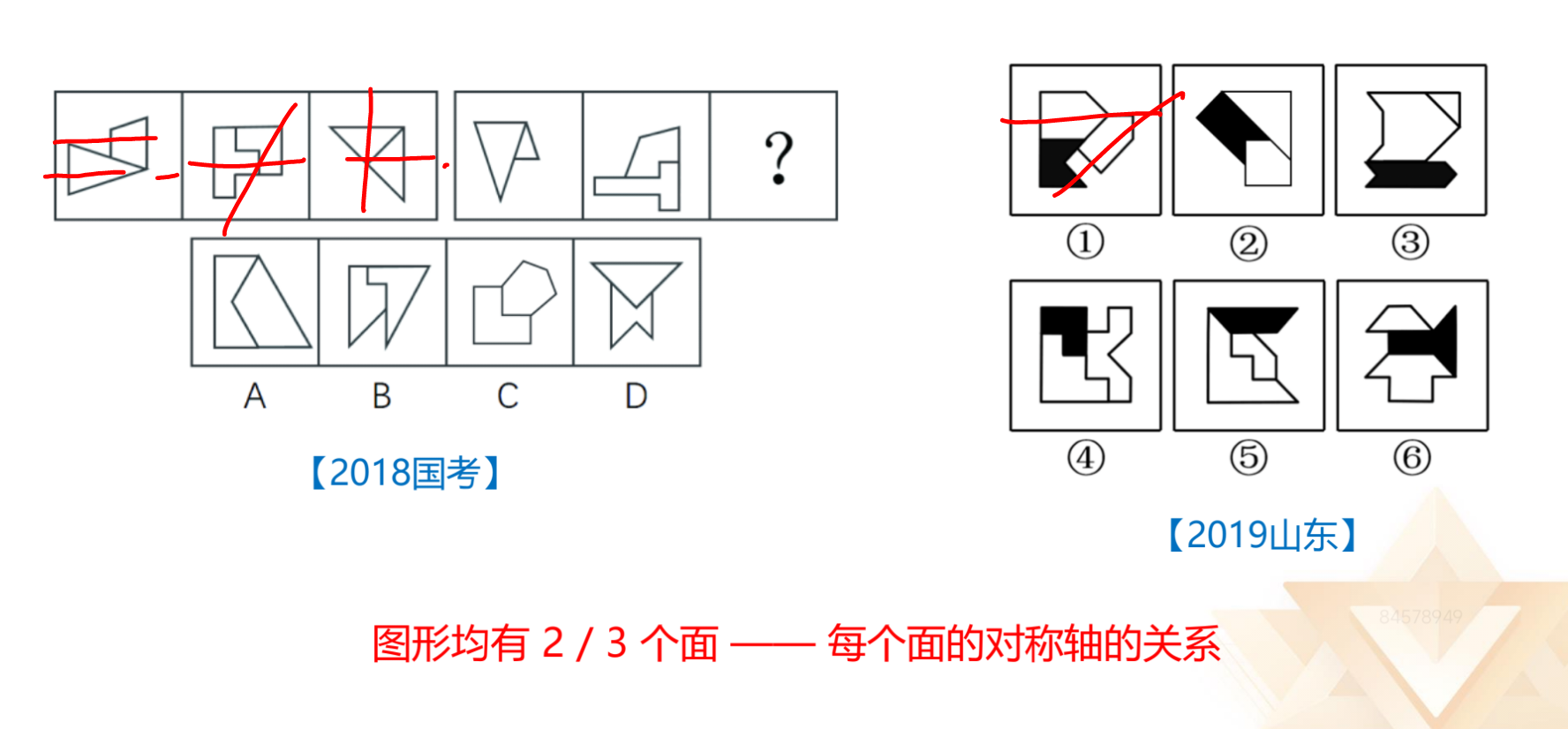
图形均有 2/3 个面,有可能考查每个面的对称轴的关系。
1.2018 年国考:考查 1 个空白面的对称轴之间的关系。
2.2019 山东:不看黑色的部分,因为黑色的不是面,只看白色的面。图①③
④对称轴相交,图②⑥对称轴平行,图⑤对称轴重合。前面讲解过,重合和平行
一般分开看,但如果没有答案,只能放在一起才能有答案,可以将重合看成一种
特殊的平行关系。
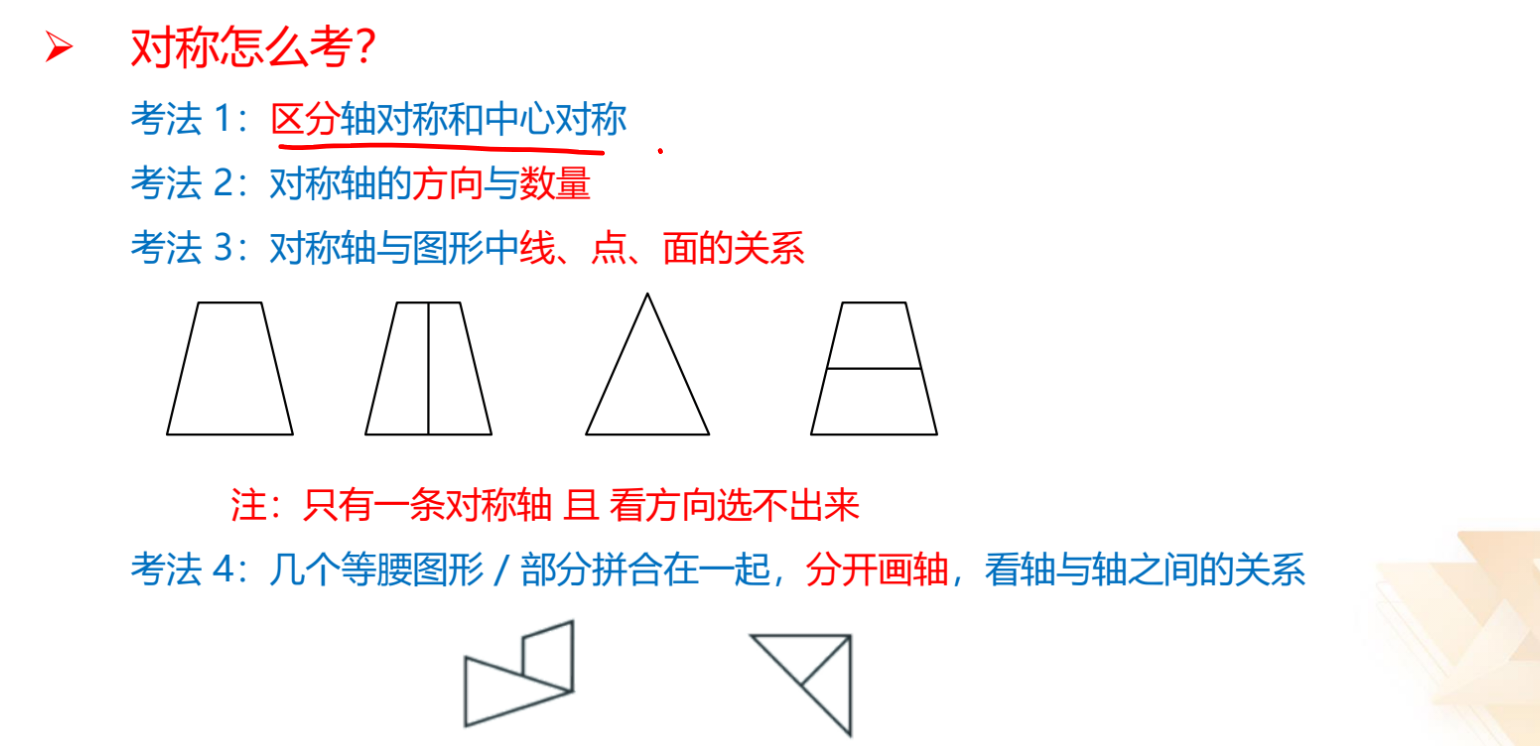
对称怎么考:
1.区分对称性。
2.对称轴的方向与数量。
3.对称轴与图形中线、点、面的位置关系,特征是图形只有 1 条对称轴。
4.不同面与不同部分之间对称轴的位置关系。
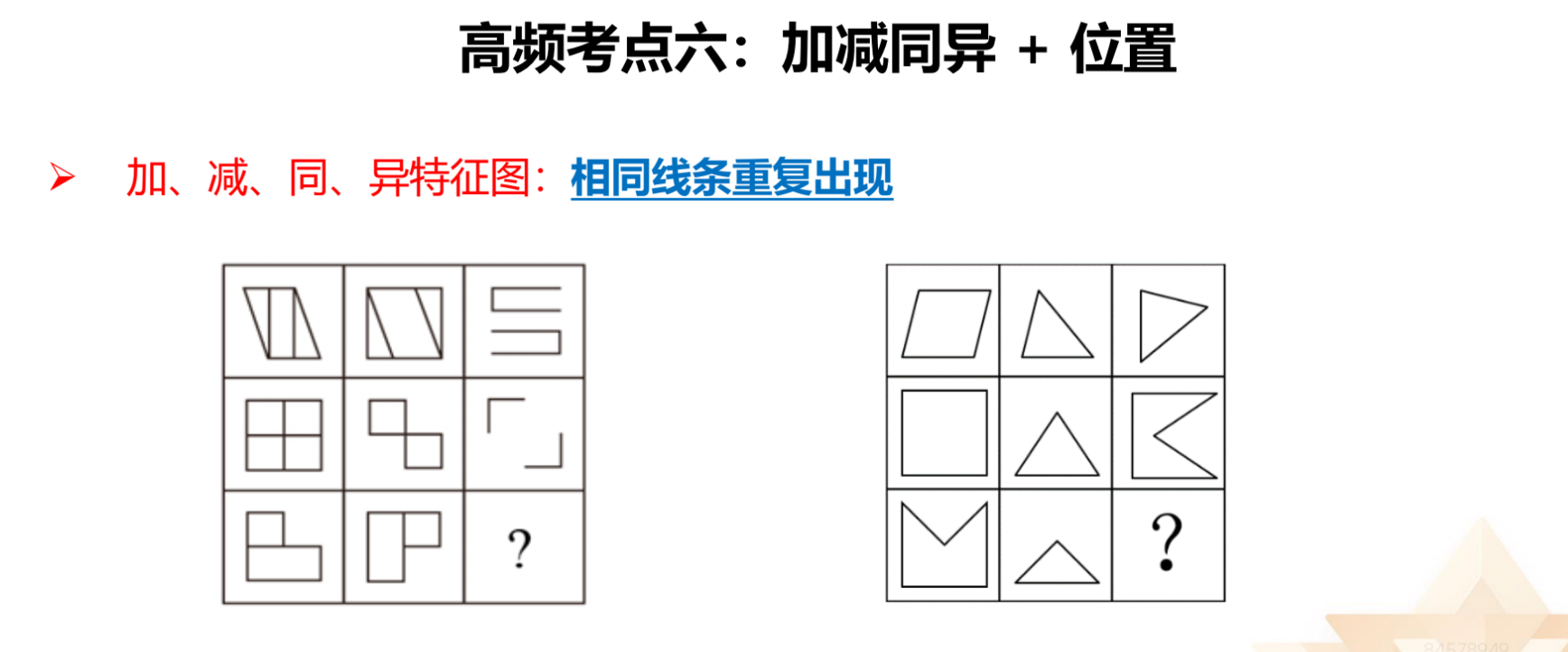
加减同异+位置:现在不能再算难题,因为考查较多。此种类型的
题目根本性考法是求同、求异,加减同异中考查相对较多的是求异,求同也有考
查,但不多。
1.如图一,第一行前两幅图有相同都相同,则没有必要先考虑转动,直接做
运算,看与第三幅图是否一样,如果一样,则不需要转动,不一样再考虑转动。
如图二,第一行图 1 和图 2 有相同线条,则先运算,运算后与图 3 不同,再考虑
转动。
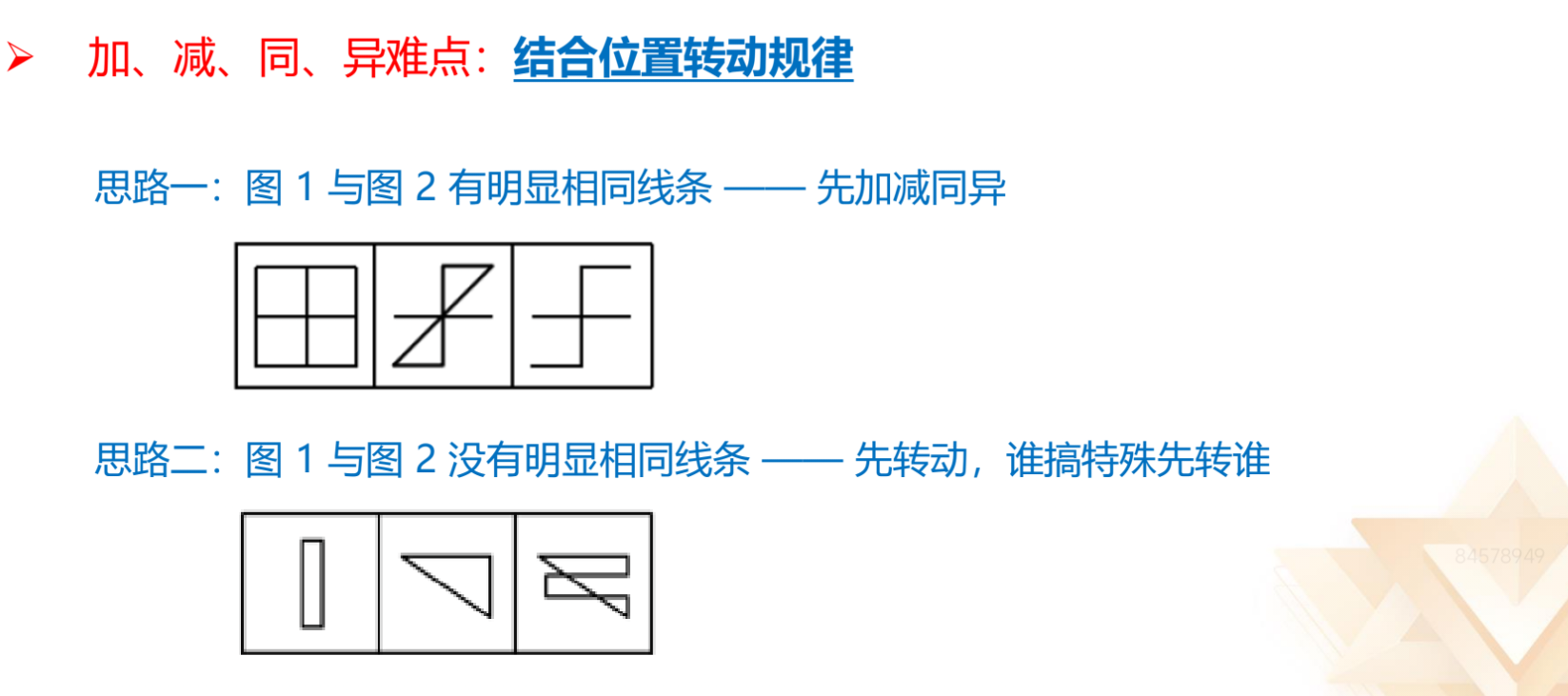
2 加、减、同、异难点:结合位置转动规律。
(1)如图三,图 1 与图 2 有明显相同线条,先不转。
(2)如图四,图 1 与图 2 没有明显相同线条,但图 2 和图 3 有相同线条,
图 1 和图 2 要运算得到图 3,但图 1 和图 2 没有相同的部分,则需要转出相同部
分,再确定相同的是留下还是去掉。与图 3 相比,谁特殊先转谁。
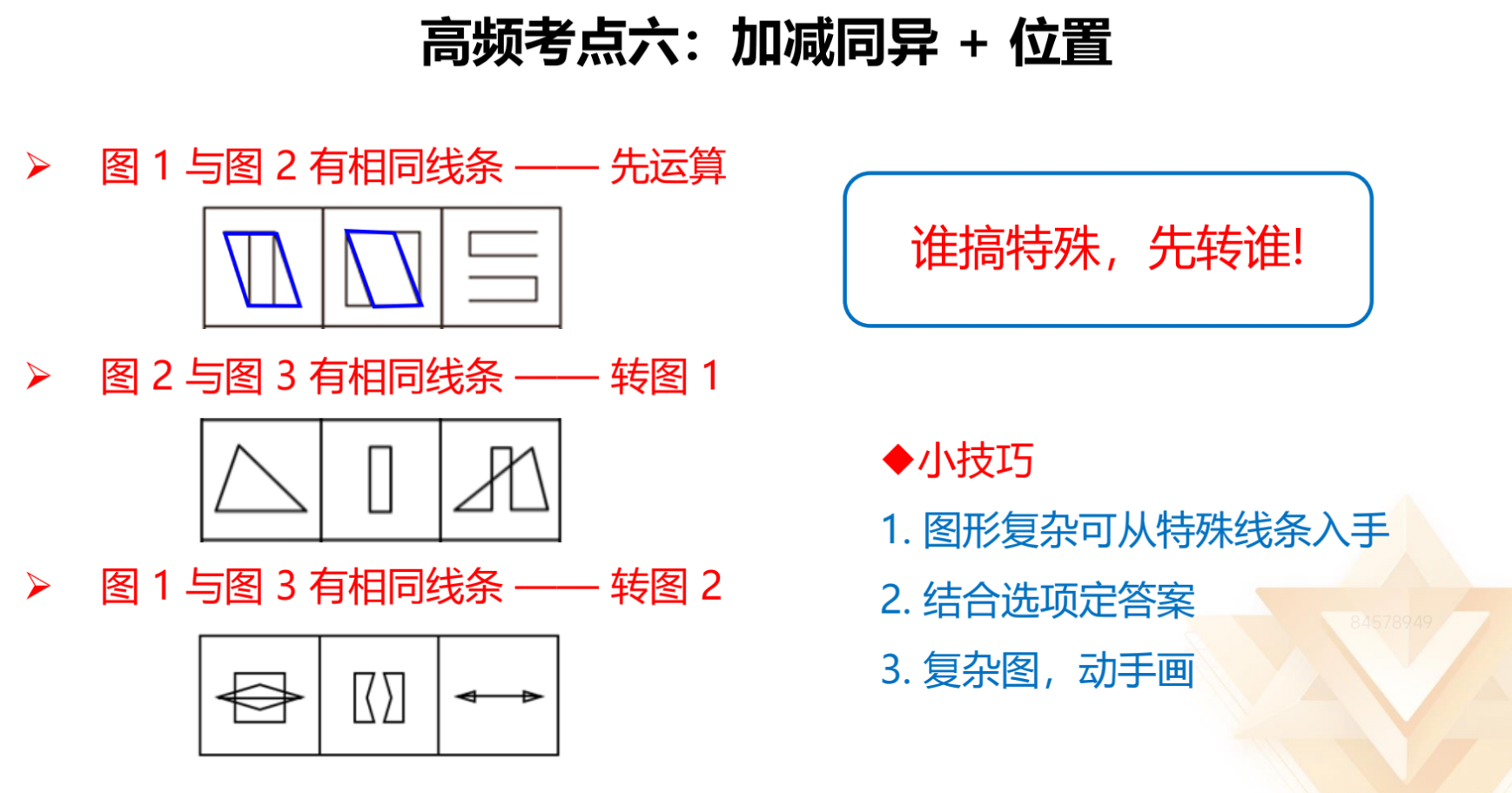
小技巧:
1.图形相对复杂时,可以从特征线条入手,建议先看横线、竖线和最长的线,
不建议先看短斜线,容易搞错方向。
2.结合选项定答案,如果有 2 个选项长一样,方向不同,则大概率需要旋转,
且答案大概率就在这两个选项中。
3.一些复杂的图需要动手画。
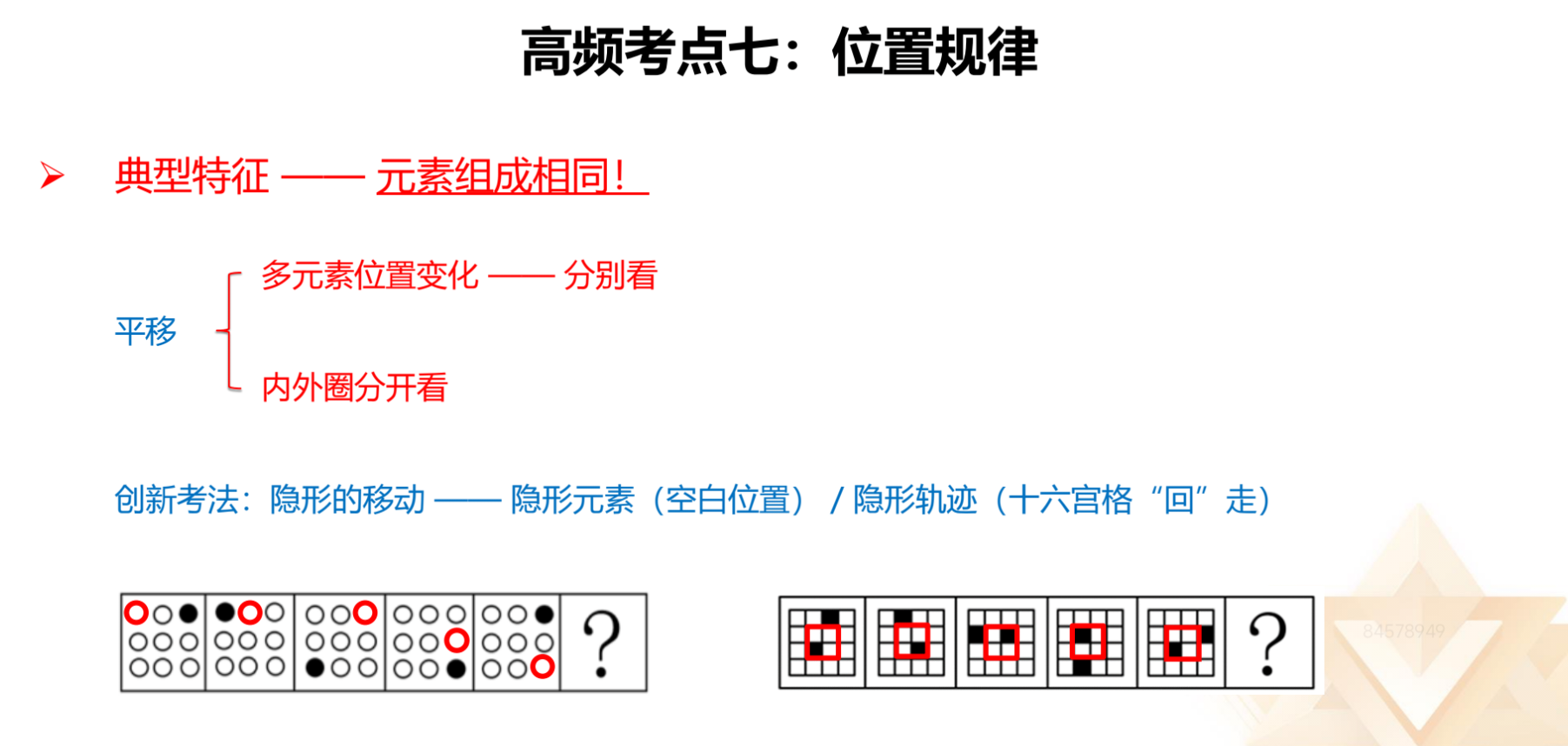
位置规律:
1.隐形元素:无论是国考还是省考,考查多个黑球、黑块平移的题目越来越
少,现在考查黑块平移一般会结合隐形元素(空白)考查,甚至有时黑白球都无
规律,只有空格有规律。遇到有黑、有空白,则多元素分开看,先看黑的或先看
空白均可以。
2.隐形轨迹:遇到 16 宫格,优先考虑内外圈分开走,即“回”字形。

命题趋势:隐藏元素、隐藏路径。
1.隐藏元素。
2.隐藏路径。
3.隐藏元素+路径,如图三,可以观察出三角形底边的移动轨迹,内部隐藏
了三角形顶点,沿着虚拟的“回”字形内圈移动

区分先转与翻转:
1.左右对称为左右翻转;上下对称为上下翻转;中心对称为旋转 180°。
2.直观看对称,左右对称最容易观察;如果将向下对称的两个图形并列画,
则不能快速看出是上下对称。;左右变、上下不变为左右翻转;上下变、左右不
变为上下翻转全变为旋转 180°。
3.如果是旋转 135.6°,则无法观察出来,尤其是结合分组分类时,更不容
易关系,所以区分旋转和翻转还有一种方法——时针法,主要应用与分组分类的
转动题
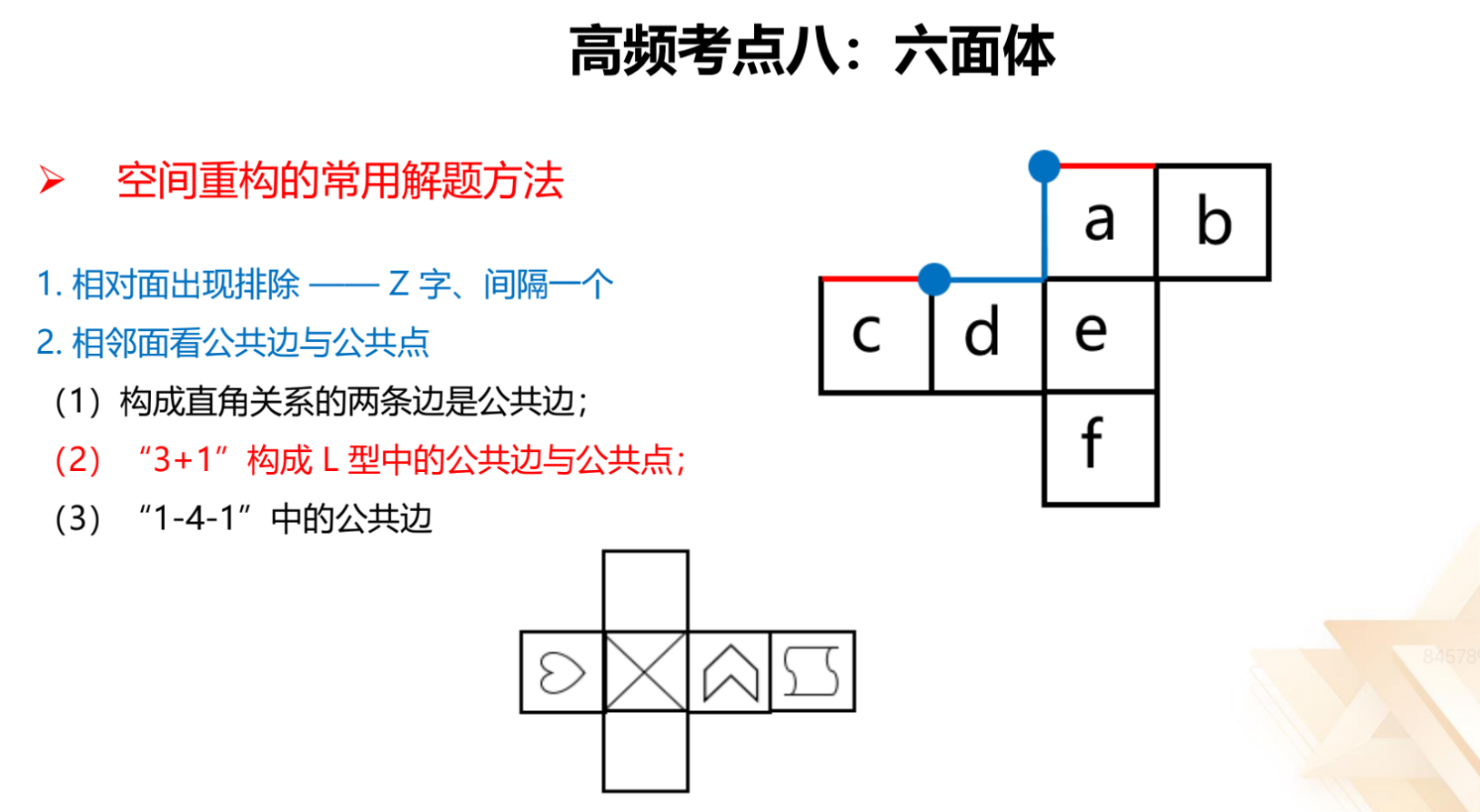
六面体:
1.相对面出现排除:
(1)同行/同列隔一个面。
(2)紧邻“Z”字中线两端,如图一,左上方的红色面和右下方的白色面不
是相对面,一定得是紧邻“Z”字中线的两个面。
2.相邻面看公共边与公共点:
(1)构成直角关系的两条边是公共边。如图二,两条蓝色的边会重合,是
面 a 和面 d 的公共边。
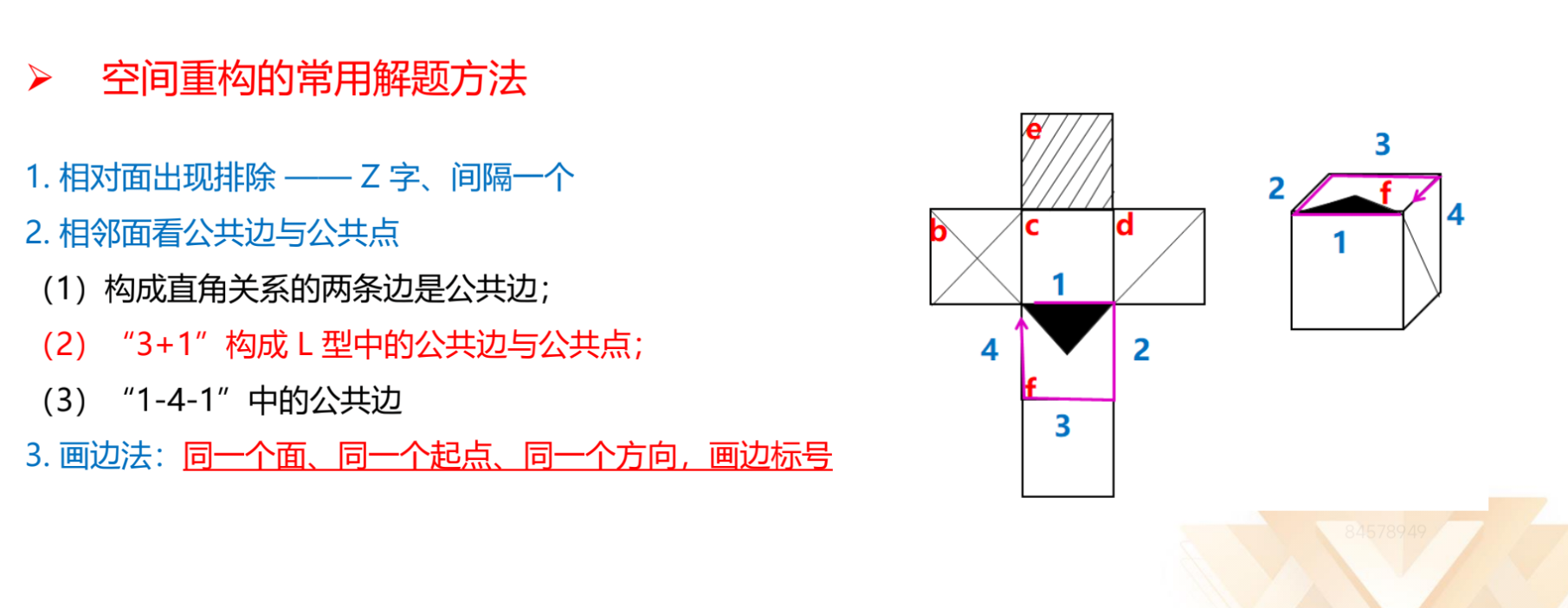
(2)“1-4-1”中的公共边:如图三,“1-4-1”形式展开图中,“4”的两侧
会重合,左右两侧的面可以互相移动。
(3)“3+1”构成“L”型中的公共边与公共点:考试中运用非常广泛。
①如图四,面 a、面 c、面 d、面 e 构成“L”型,3 个面与 1 个面构成的“L”
叫做“3+1”的“L”型。从“L”的直角点出发,第一条边重合,第二条边也重
合,与边 1 重合的是边 2;与 3 重合的是边 14;与边 5 重合的是边 8;与边 6 重
合的是边 7;与边 9 重合的是边 12;与边 10 重合的是边 11;此时剩余边 4 个边
13,则这两条边相互重合。此方法涉及移面的法则,但讲解移面的意义不大,大
家只需记住一点,即无论在哪个“3+1”的“L”型中,同方向的两条边重合,可
以锁定相对较远的两个面的公共边。
②如图五,“3+1”的“L”型中,从“L”的直角点出发,第一个点重合,第
二个点也重合,因此两个红点是同一个点,说明该点既在面 a 中,又在面 b 中,
也在面 c 中,即面 a、面 b 和面 c 的公共点。
③如图六,距离最远的三个面是面 b、面 c、面 f,面 a、面 b、面 e、面 f
构成“3+1”的“L”型,从直角点出发,点 1 和点 2 重合,点 3 和点 4 重合。在
面 c、面 d、面 e、面 f 构成的“L”中,点 5 和点 6 重合,点 7 和点 3 重合。点
3 和点 4、点 7 重合,即三个点都会重合,是同一个点,既在面 f 中,又在面 c
中,也在面 b 中,即面 b、面 c 和面 f 的公共点。
④学会此方法后可以确定距离最远的面的公共边和公共点,可以帮助解决难
题,简单题用不到,该知识点比较难,下节课会再次讲解。
3.画边法:
(1)同一个面、同一个起点、同一个方向,画边标号。如图七,均以黑色
三角形的底边为唯一边在黑三角形面中画边,顺时针画边并标号 1-4,展开图中
边 4 挨着“×”面,立体图形中边 4 挨着斜线面,故立体图形错误。
(2)如图八,不容易确定唯一点、唯一边。面 a 和面 b 的公共边是唯一的,
因为六面体中两个面只能有 1 条公共边。以面 a 和面 b 的公共边为起点,在面 a
中顺时针画边并标号 1-4,立体图形中边 2 挨着面 c,而展开图中边 2 挨着空白
面,故展开图错误。没有唯一边,也可以用公共边构造出唯一边进行画边,此方
法结合“3+1”的“L”型就可以实现在图形中即使没有唯一点和唯一边,仍然可
以用画边法解题。
(3)如图九,面 a、面 b、面 c 的公共点也是唯一的,由公共点出发在面 a
中顺时针画边并标号 1-4,结合“3+1”的“L”型找出选项的公共点,立体图形
中边 1 挨着面 c,展开图中边 1 挨着面 b,故可以排除。
(4)可能会认为画边法有局限性,并不是所有图形都可以找到唯一点、唯
一边,其实不然,如果能够结合找唯一点和唯一边的方法,可以构造出公共点或
公共边作为唯一点或唯一边。考试时只要掌握空间重构的方法,且将方法熟练应
用,则能够解决很多问题
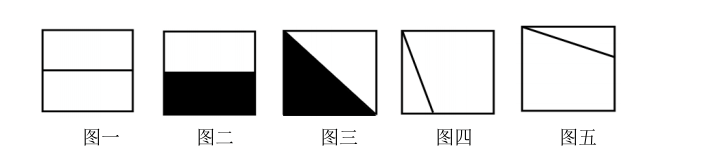
常见的面:
1.如图一,内部有 1 很线条,考查的是该线条与另一个面是平行还是垂直。
升级版图图二,面内一半黑、一半白,仍然可以考查平行和垂直;还可以考查颜
色,即黑色挨着什么、白色挨着什么;也可以考查画边法,因为有黑色的边是唯
一边。
2.如图三,面内 1 条斜线,一半黑、一半白,可以考查颜色,看黑边挨着什
么,白边挨着什么;其次可以考查画边,因为有唯一的黑色直角点。
3.如图四,面内部有 1 个小直角三角形,首先可以考查边长、短直角边,看
公共边是挨着短直角边还是挨着长直角边;其次可以考查画边法,因为直角点可
以作为唯一点;第三可以考查区分,即与图五的区分,图四和图五不同,但出现
在题目中可能会觉得是一样的。区分时,从直角点出发,顺时针标 1,图四中 1
是长直角边,图 5 中 1 是短直角边,结合了长直角边、短直角边和画边。
六面体:最重要的是“L”型中的公共边与公共点。
今日总结
今日总结:
1.面的细化:所有面形状、相同形状的面、最大/最小面。
2.线:
(1)特征:单一线条、规则多边形。
(2)曲直分开、内外分开、横竖分开,分开看不行,则做运算。
(3)平行线。
(4)笔画数(高频考法)。
3.点:除了曲直交点和内外交点,不要忘记切点。
4.样式规律:是否旋转取决于前两幅图中是否有相同线条。
5.位置规律:可能会考查空白元素、旋转与翻转的区分。
6.对称性:1 条对称轴先看方向,再看对称轴经过的部分;如果有 2 条及以
上对称轴,可以看数量和是否为轴+中心对称。
7.空间类:
(1)主要引入了两个重点内容,第一是“3+1”的“L”中公共点与公共边
如何确定,以及通过“3+1”的“L”的公共点和公共边能否进一步帮助使用画边
法做题。
(2)有一些考试中常见的面,要知道遇到什么样的面应该用什么样的方法
快速做题。