强化训练-数量1

【注意】代入排除：
1.何时用？
    （1）题型：年龄、余数、多位数、不定方程。
    （2）选项：选项信息充分，出现“分别”、“各”字样。
2.怎么用？
    （1）先排除：大小、奇偶、倍数、尾数。
    （2）再代入：
        ①最值原则。
            a.问最大，从最大开始代入。
            b.问最小，从最小开始代入。
    ②从简原则：简单条件、好算选项。
3.代入逻辑：遇到矛盾，就排除；全部满足，就选择。

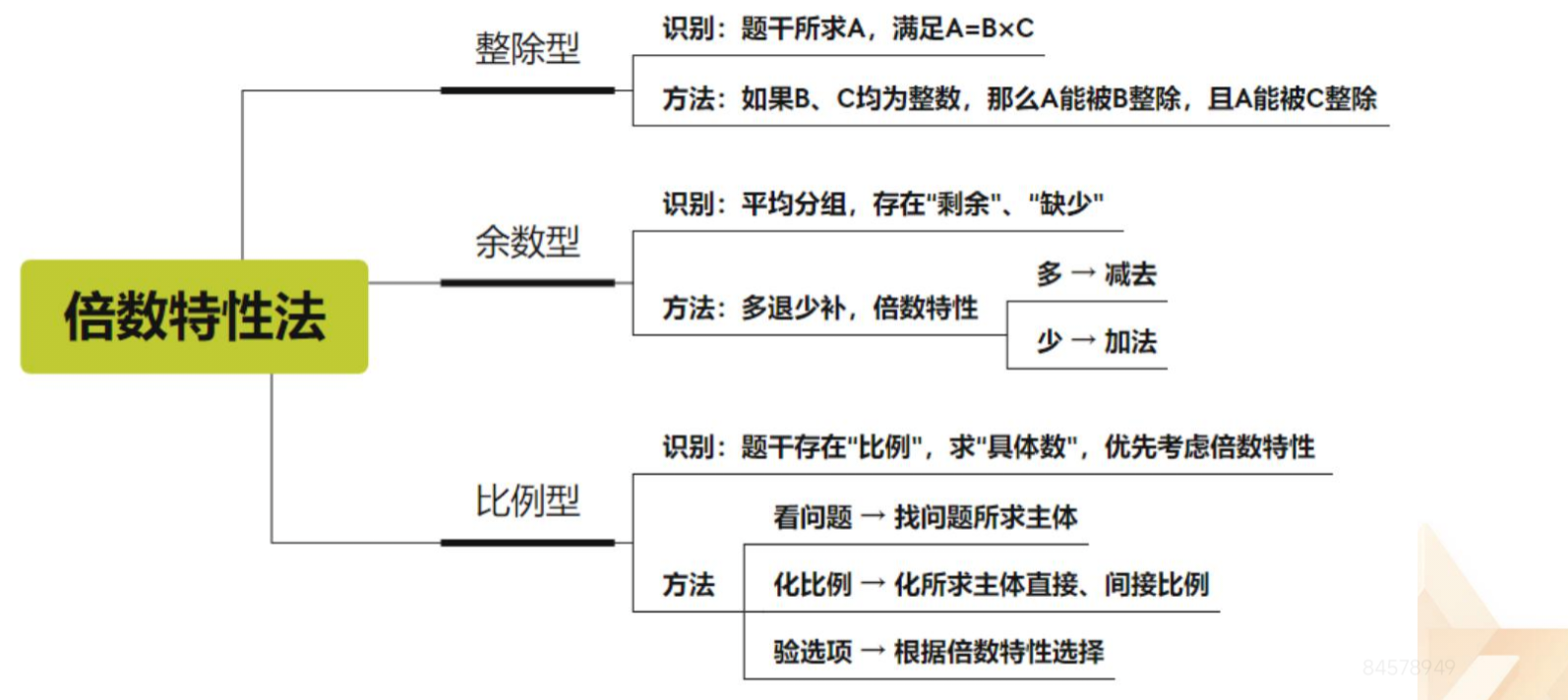
【注意】倍数特性法：
1.整除型：更多的是一种猜题的逻辑。
    （1）识别：题干所求 A，满足 A=B*C。例如问的是路程，S=v*t，可以猜 S
是 v 或者 t 的倍数；再例如问的是总量，总量=效率*时间，可以猜总量是效率或
者时间的倍数。
    （2）方法：如果 B、C 均为整数，那么 A 能被 B 整除，且 A 能被 C 整除。
2.余数型：考点（套路题）。例如 y=ax+b，如何才能平均分配？y-b=ax。
    （1）识别：平均分组，存在“剩余”、“缺少”。
    （2）方法：多退少补（平均分配），倍数特性，多→减法；少→加法。
3.比例型：
    （1）识别：题干存在“比例”，求具体数，优先考虑倍数特性。
    （2）方法：看问题，找问题所求主体；化比例，化所求主体直接、间接比
例（A/B=m/n，m/n 是最简分数，A 是 m 的倍数，B 是 n 的倍数，A+B 是 m+n 的倍
数，A-B 是 m-n 的倍数）；验选项，根据倍数特性选择。
    （3）如果题目给出比例，求比例，可以用赋值法；如果给比例求的是具体
数值，优先考虑倍数特性，实在不行再列方程。

【知识点】余数问题的三种延伸考法——口诀：余同取余，和同加和，差同
减差，公倍数做周期。
1.余同取余，例如“一个数除以 7 余 1，除以 6 余 1，除以 5 余 1”，可见，
所得余数恒为 1，则取 1，被除数的表达式为 210n+1。注意：210 为各个除数的
最小公倍数。
2.和同加和，例如“一个数除以 7 余 1，除以 6 余 2，除以 5 余 3”，可见，
除数与余数的和相同，取此和 8，被除数的表达式为 210n+8。
3.差同减差，例如“一个数除以 7 余 3，除以 6 余 2，除以 5 余 1”，可见，
除数与余数的差相同，取此差 4，被除数的表达式为 210n-4。

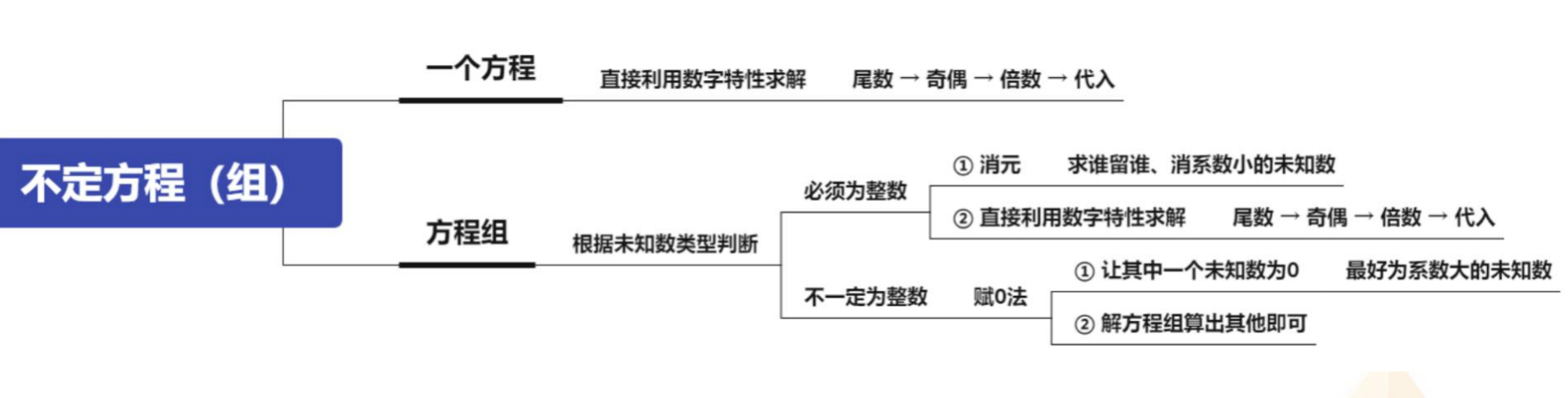
【注意】不定方程（组）：
1.一个方程：直接利用数字特性求解，尾数→奇偶→倍数→代入。
2.方程组：根据未知数类型判断。
    （1）必须为整数：
        ①消元，求谁留谁，消系数小的未知数。
        ②直接利用数字特性求解，尾数→奇偶→倍数→代入。
    （2）不一定为整数，赋 0 法。
        ①让其中一个未知数为 0，最好为系数大的未知数。
        ②解方程组算出其他即可。

【注意】常规工程：
1.完工时间型：
    （1）识别：
        ①总量、效率、时间中，只给了时间具体量。
        ②两个及以上的完工时间。
        ③完工时间：直接或间接，只要能推算出完成工作所需时间即可。
    （2）方法：
        ①第一步，赋总量：完工时间的公倍数。
        ②第二步，求效率：效率=总量/时间。
        ③第三步，再做题：根据工作过程列式。
2.效率比例型：
    （1）识别：
        ①题干直接给出效率的比例关系。
        ②两种工作方式完成相同的工作总量，可推出效率比例。
    （2）方法：
        ①第一步，赋效率，对应比例。
        ②第二步，求总量，总量=效率*时间。
        ③第三步，再做题，根据工作过程列式。
3.给具体量型：
    （1）识别：除时间外，效率或总量给出具体值。
    （2）方法：
        ①设未知数。
        ②再做题→听话即可。

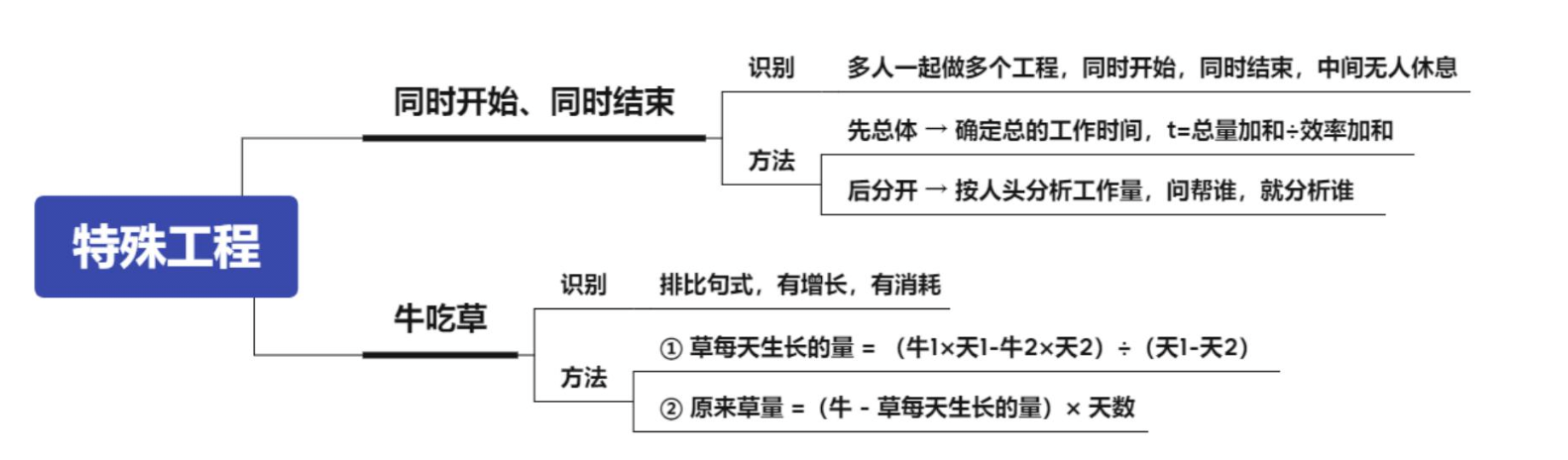
【注意】特殊工程：
1.同时开始、同时结束：
    （1）识别：多人一起做多个工程，同时开始，同时结束，中间无人休息。
    （2）方法：
        ①先总体→确定总的工作时间，t=总量加和/效率加和。
        ②后分开→按人头分析工作量，问帮谁，就分析谁。
2.牛吃草：
    （1）识别：排比句式，有增长，有消耗。
    （2）方法：
        ①草每天生长的量=（牛 1*天 1-牛 2*天 2）/（天 1-天 2）。
        ②原来草量=（牛-草每天生长的量）*天数。

【知识点】交替工作：
1.例：失乐志一天搬 8 块，鸡汤照一天搬 10 块，现需要搬 100 块，两人一
替一天工作，问：至少需要几天完成？
答：总量有 100 块，两人交替工作，按照周期做，每天工作量分别为：8、
10、8、10，2 天为 1 个周期，1 个周期的工作量=10+8=18，100/18=5……10，5
个周期有 10 天，剩余 10 个工作量，失乐志一天只能做 8 个，需要 2 天做完剩余；
如果剩余 10 个工作量都给鸡汤照做，一天就能做完，所以最少需要 10+1=11 天。
2.方法：
（1）第一步，确定总量与周期内工作量。
（2）第二步，求周期，算余数（剩余工作量）。
（3）第三步，分析剩余工作量

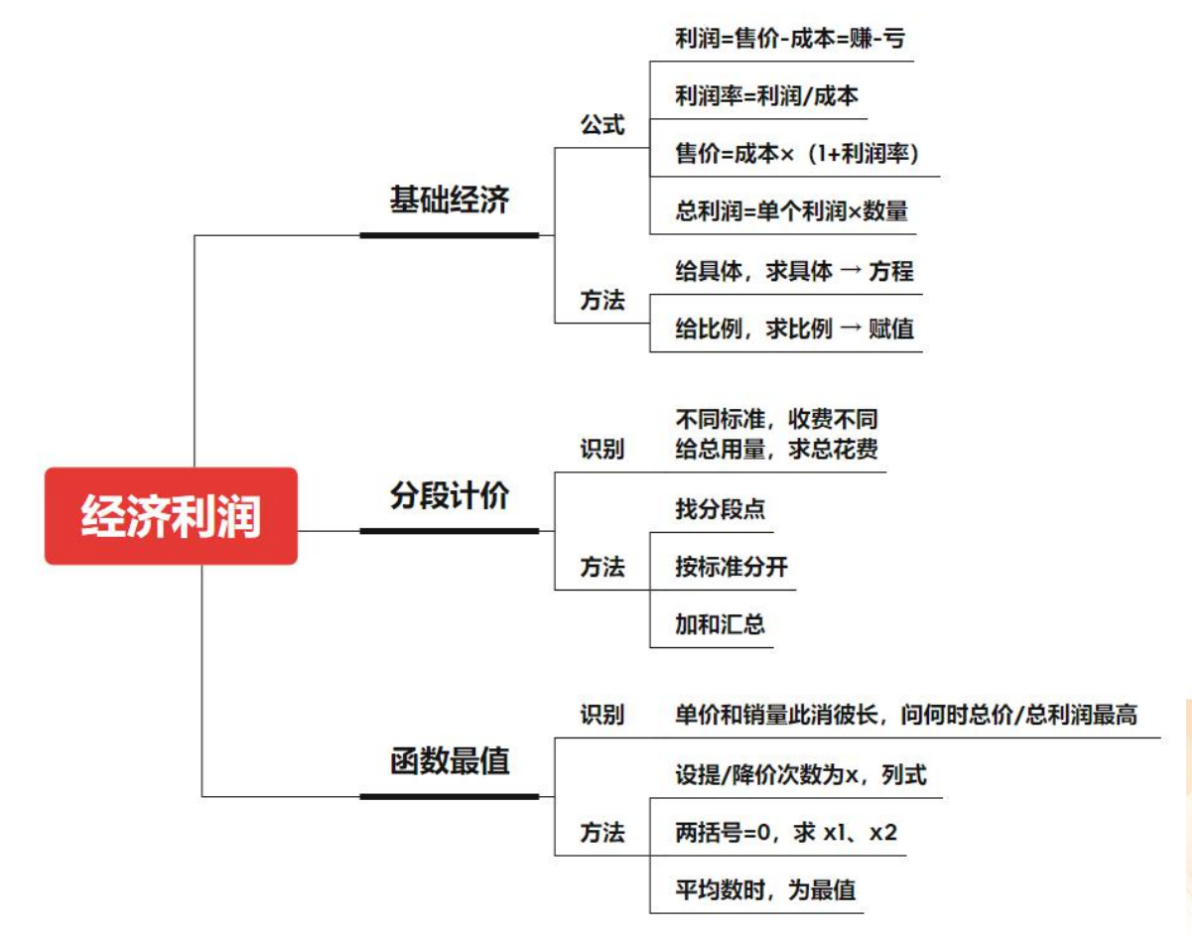
【知识点】经济利润问题：
1.基础经济：破题点是方法的选择。
    （1）公式：利润=售价-成本=赚-亏；利润率=利润/成本；售价=成本*（1+
利润率）；总利润=单个利润*数量。
    （2）方法：
        ①给具体，求具体→方程。
        ②给比例，求比例→赋值。
2.分段计价：
    （1）识别：不同标准，收费不同；给总用量，求总花费。
    （2）方法：找分段点；按标准分开；加和汇总。
3.函数最值：
    （1）识别：单价和销量此消彼长，问何时总价/总利润最高。
    （2）方法：
        ①设提/降价次数为 x，列式。
        ②两括号=0，求 x1、x2。
        ③平均数时，为最值

【知识点】合并付费：
1.两人均达到最高折扣→谁为基础都可以。
2.一人达到，一人未达到→以达到的为基础，求未达到的原价。
3.两人均未达到→求原价再计算，然后合并。
4.例：买东西，500 元以下打九折，500 元以上打八折。
    （1）甲付款 490 元，乙省了 120 元，若两人合并付费，省多少钱？
答：如果 500 元打九折，是 450 元，甲付了 490 元，比 450 元多，说明达到
了最高折扣八折；以 500 元为分界线，打九折省了 500*10%=50 元，乙省了 120
元，比 50 元多，说明乙也达到了最高折扣八折，两个人都达到最高折扣，以谁
作为基础都无所谓，如果把甲作为基础，乙接在后面，则甲没有变化，乙原来打
九折的部分，现在打八折，省了一折，即 500*0.1=50 元。
    （2）甲付款 490 元，乙付款 360 元，若两人合并付费，省多少钱？
答：甲达到最高折扣八折，乙没有达到，若一人达到，一人未达到，以达到
的为基础，求未达到的原价。甲没有变，乙原价是 360/0.9=400 元，现在可以打
八折，省一折，即 400-360=40 元。
    （3）甲付款 360 元，乙付款 270 元，若两人合并付费，省多少钱？
答：两人均未达到，求原价再计算，然后合并。甲原价为 400 元，乙原价为
300 元，若合并付费，450+160=610 元，原来是 360+270=630 元，差了 630-610=20
元。