梳理课
Last updated on
一、基础运算
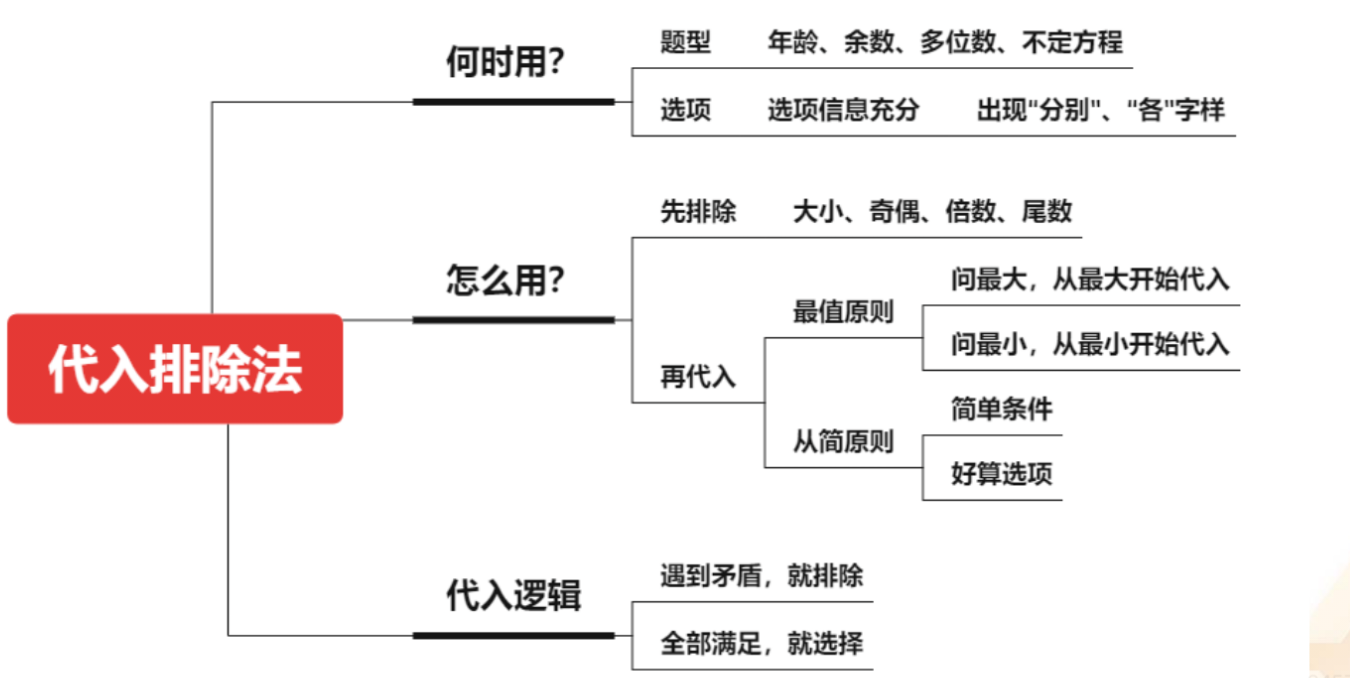
1.何时用:
(1)题型:年龄、余数、多位数、不定方程。其中年龄、多位数用的时候
往往是纯代入,技巧性不多;余数、不定方程可能需要先排除(根据数字特性排
除),再代入。
(2)选项:选项信息充分,出现“分别”、“各”字样。
2.怎么用:
(1)先排除:大小、奇偶、倍数、尾数。
(2)再代入:
①最值原则:问最大,先代最大;问最小,先代最小。如果题目中出现正相
关,如前面的剩 20 的题目,代入的量大,剩的多,代入的量少,剩的少,则居
中代入;如果没有最值,也没有正相关,往往选 A 项和 B 项的概率比较大,出题
人考的不是计算,考的是能不能把题目梳理明白。
②从简原则:简单条件;好算选项。
3.代入逻辑:
(1)遇到矛盾,就排除。
(2)全部满足,就选择。
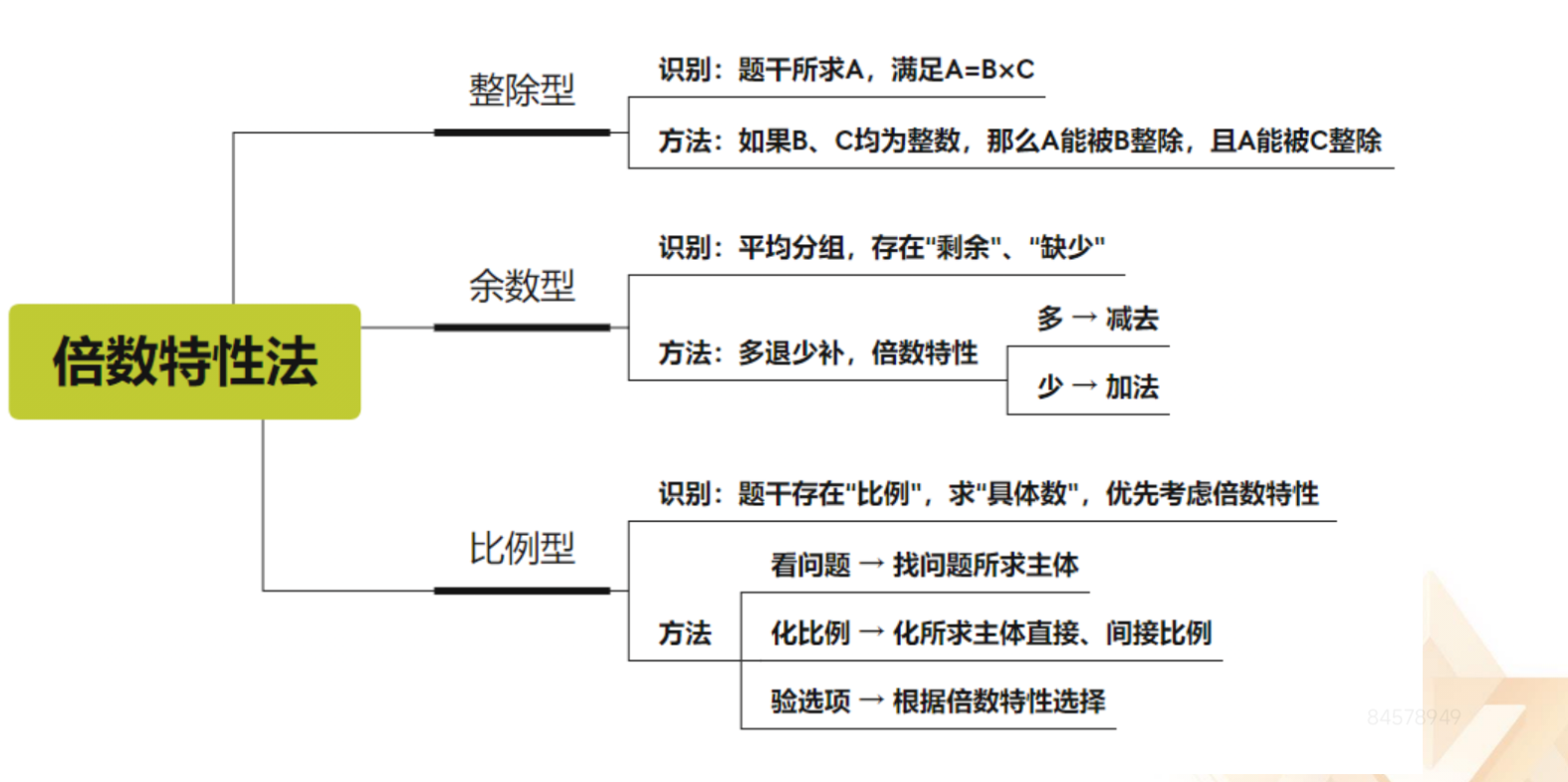
1.整除型:用的比较少。
(1)识别:题干所求 A,满足 A=B*C。当主体必须为整数,那么正常做,如
果主体可以不为整数,那么就猜。如:做一批零件,18 小时完成,则总量为 18*
效率,总量为整数,效率也是整数,所以总量为 18 的倍数,如果路程 S=VT,猜
S 是 V、T 的倍数时,就要小心,V、T 不一定为整数。
(2)方法:如果 B、C 均为整数,那么,A 能被 B 整除,且 A 能被 C 整除。
2.余数型:
(1)识别:平均分组,存在“剩余”、“缺少”。
(2)方法:多退少补,倍数特性。多→减去;少→加法。如:平均每人 3
个,还剩 2 个,总数-2=3 的倍数。
3.比例型:
(1)识别:题干存在“比例”,求“具体数”,优先考虑倍数特性。
(2)方法:
①看问法:找问题所求主体。
②化比例:化所求主体直接、间接比例。
③验选项:根据倍数特性选择。
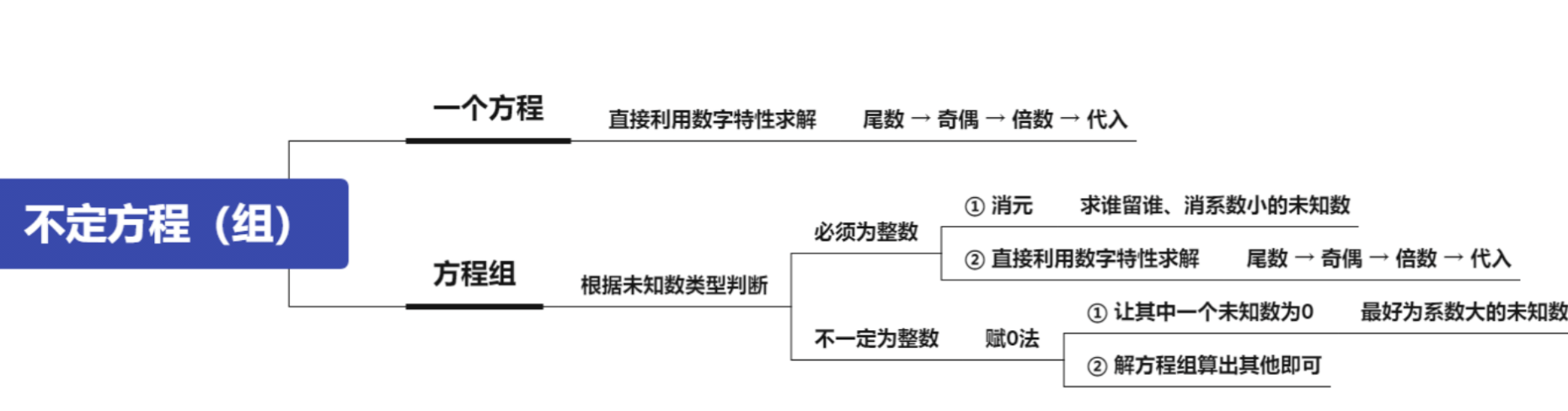
1.如果列出的是一个方程:直接利用数字特性求解,尾数→奇偶→倍数→代
入。
(1)尾数是 0 或 5 的时候用尾数法,遇到 5 时乘以 2 转化为 0 分析。
(2)x、y 前面的系数一奇一偶的时候用奇偶,从偶系数入手分析。
(3)存在共同的因子时考虑倍数。
(4)前面三种方法都行不通,就代入。
2.方程组:根据未知数类型判断。
(1)必须为整数:
①消元:求谁留谁,一般消系数小的未知数,转化为一个不定方程。
②直接利用数字特性求解,尾数→奇偶→倍数→代入。
(2)不一定为整数:赋 0 法。
①让其中一个未知数为 0,最好为系数大的未知数。
②解方程组算出其他即可。
二、工程问题
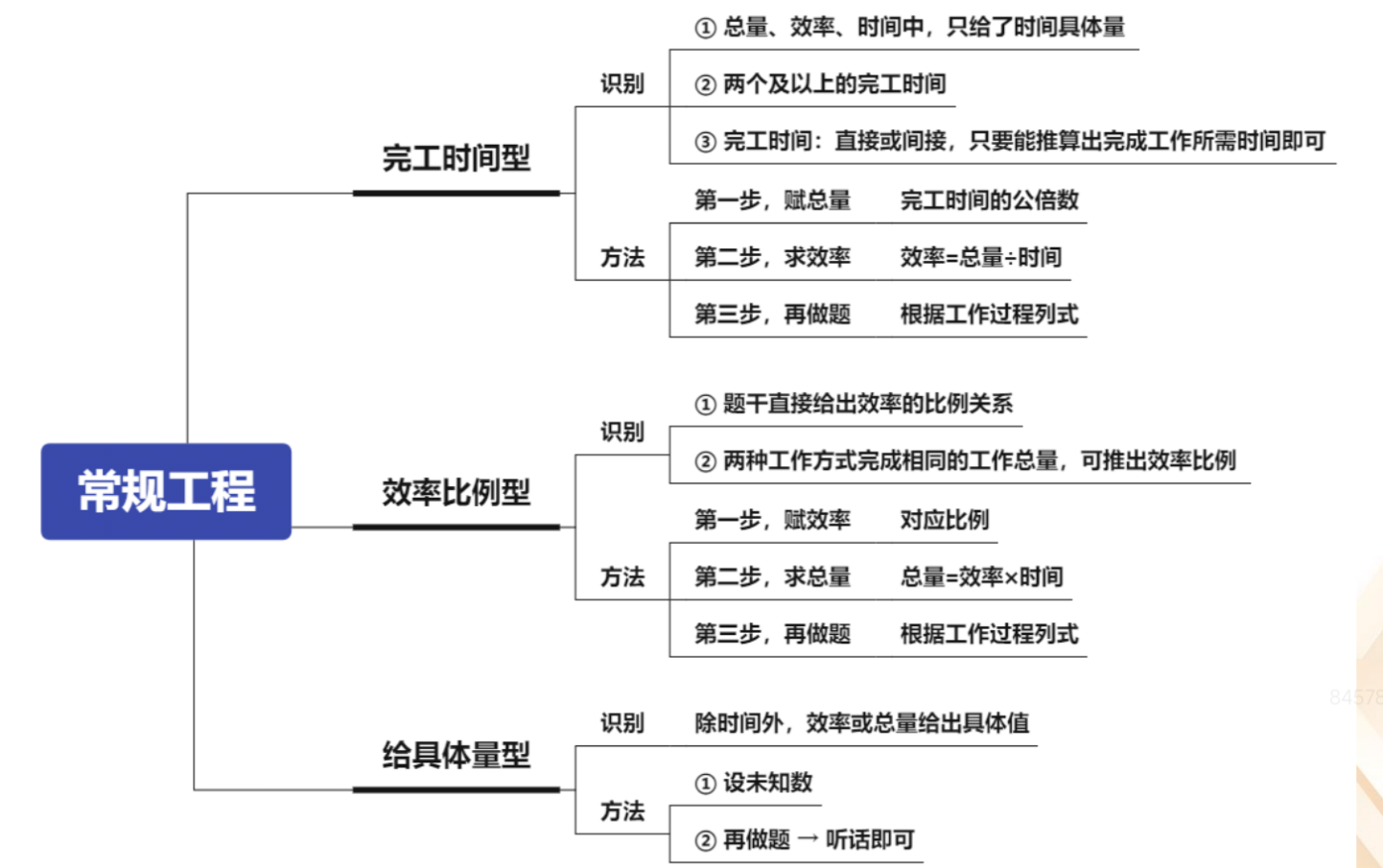
1.完工时间型:
(1)识别:
①总量、效率、时间中,只给了时间具体量。
②两个及以上的完工时间,一个时间不行。
③完工时间:直接或间接,只要能推算出完成工作所需时间即可。
(2)方法:
①第一步,赋总量:赋值时间的最小公倍数,完工时间的公倍数。
②第二步,求效率:效率=总量/时间。
③第三步,再做题:根据工作过程列式。
2.效率比例型:
(1)识别:
①题干直接给出效率的比例关系。如:甲比乙多 1/4,甲/乙=5/4,可以赋
值甲为 5,乙为 4。
②两种工作方式完成相同的工作量,可推出效率比例。如:一项工程,甲 3
天乙 4 天可以完成,甲 2 天乙 6 天也可以完成,则 3 甲+4 乙=2 甲+6 乙,甲=2
乙,所以甲/乙=2/1。
(2)方法:
①第一步,赋效率:对应比例。
②第二步,求总量:总量=效率*时间。
③第三步,再做题:根据工作过程列式。
3.给具体单位型:
(1)识别:除时间外,效率或总量给出具体值。
(2)方法:
①设未知数。
②再做题→听话即可。
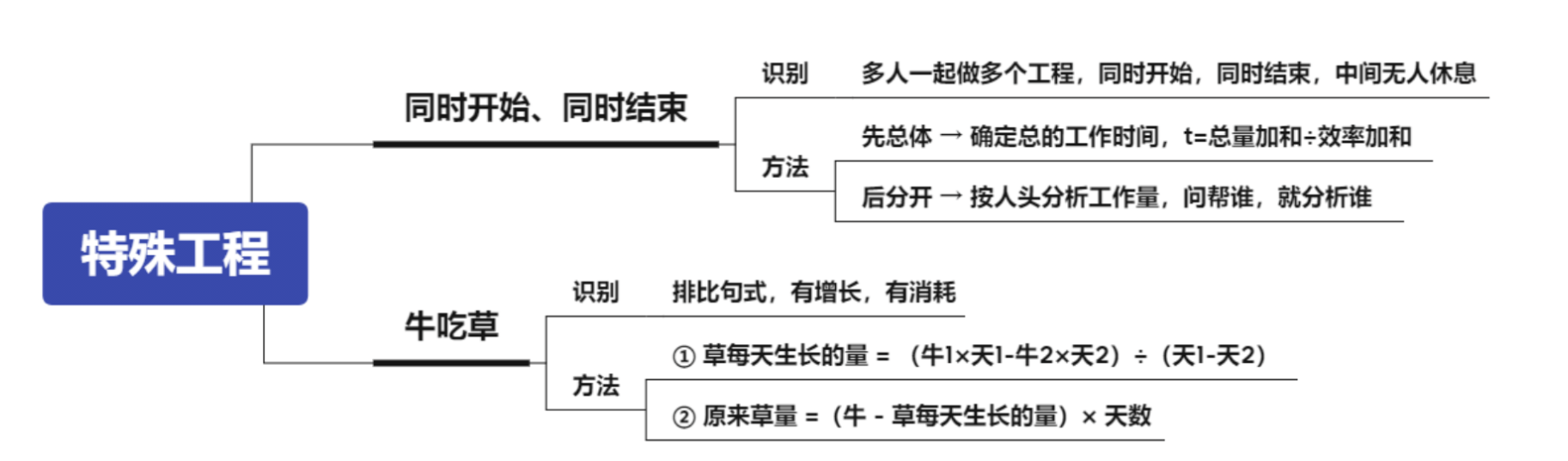
1.同时开始、同时结束。
(1)识别:多人一起做多个工程,同时开始,同时结束,中间无人休息。
(2)方法:
①先总体:确定总的工作时间,t=总量加和+效率加和。
②后分开:按人头分析工作量,问帮谁,就分析谁。如:问帮甲多少,甲负
责 A 部分,A 一部分是甲做的,一部分是帮他的丙做的,A 减去甲的时间*效率剩
下的就是丙的量,再除以效率就是时间。
2.牛吃草:
(1)识别:排比句式,有增长,有消耗。
(2)方法:
①草每天生长的量=(牛 1*天 1-牛 2*天 2)÷(天 1-天 2)。注意天 1-天 2
的顺序要一致,分子是天 1-天 2,那么分母也是天 1-天 2。
②原来草量=(牛-草每天生长的量)*天数。
三、经济利润问题
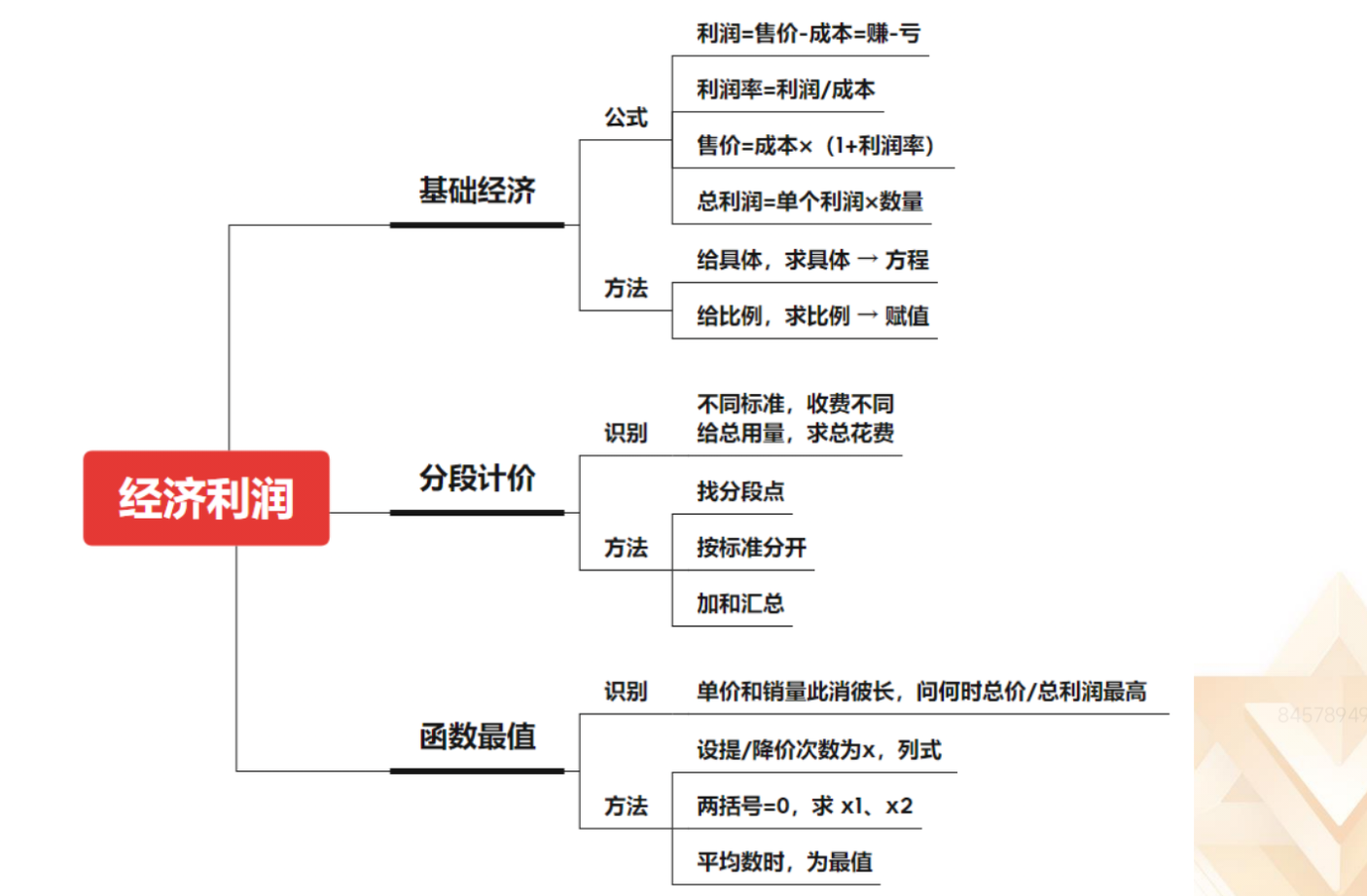
1.基础经济:
(1)公式:
①利润=售价-成本,多用于列式。有同学可能喜欢用赚-亏,但是尽量不要
用,因为有同学会只想到赚,没想到亏。
②利润率=利润/成本,资料分析中利润率是利润/收入。
③售价=成本*(1+利润率)。
④总利润=单个利润*数量。
(2)方法:
①给具体,求具体→列方程。
②给比例,求比例→赋值。赋值课上讲的不多,建议大家听一下专项课中的
赋值法。
2.分段计价:
(1)识别:不同标准,收费不同。给总用量,求总花费。
(2)方法:找分段点,按标准分开,加和汇总。
3.函数最值:
(1)识别:单价和销量此消彼长,问何时总价/总利润最高。如:原来卖 5
元,可以卖出 100 个,每增加 1 元,少卖出 10 个,设增加 x 次,5+1*x,100-10x,
令 5+1*x=0,100-10x=0,解得 x1=-5,x2=10,求平均数时,为最值,(-5+10)/2=2.5,
2.5 距离 2 和 3 的距离都一样,所以取哪个都可以;如果算出是 2.7,距离 3 较
接近,所以在 3 的位置最高。
(2)方法:
①设提/降价次数为 x,列式。
②两括号=0,求 x1,x2。
③平均数时,为最值。
四、行程问题
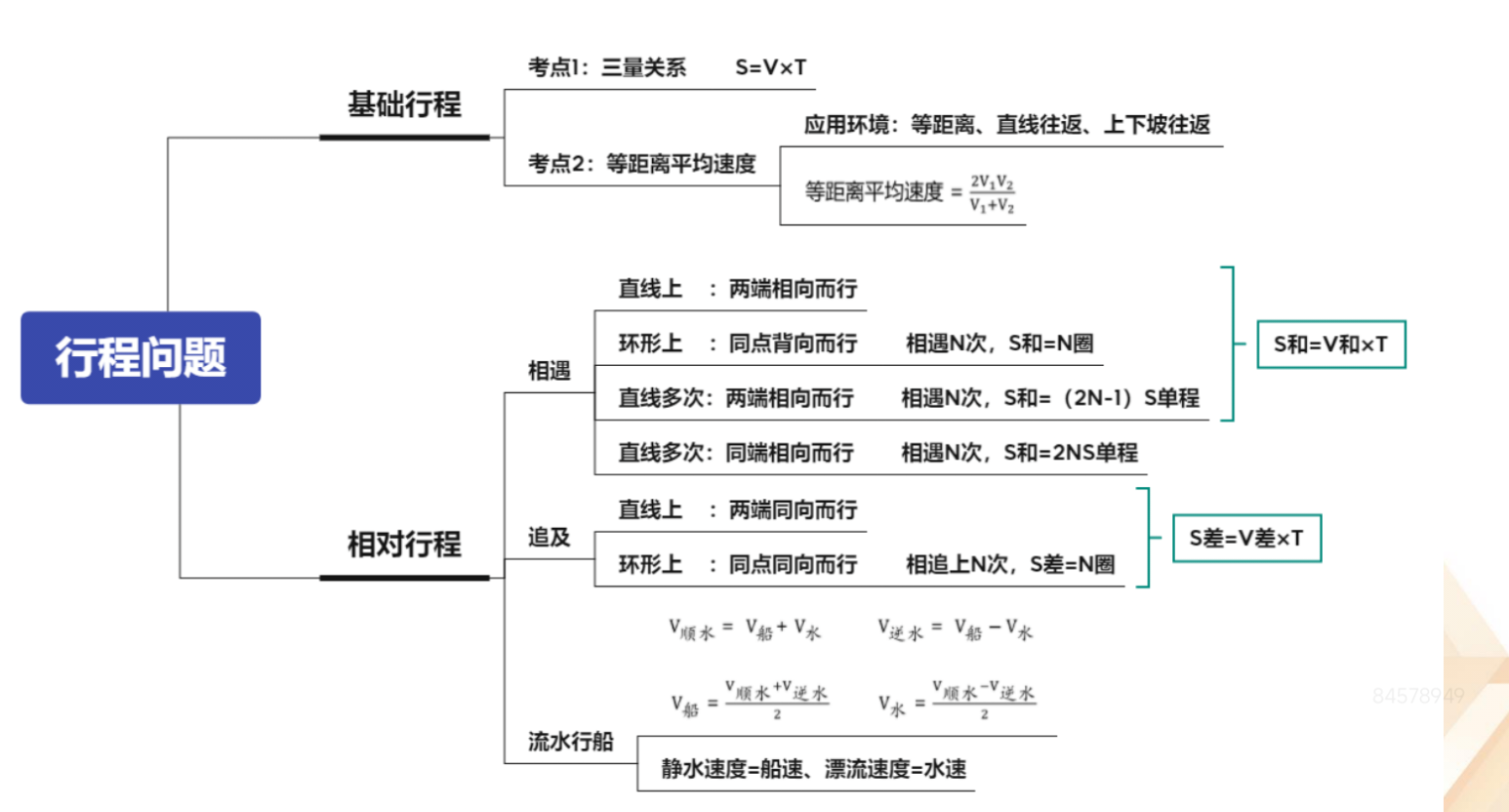
1.基础行程:
(1)考点 1:三量关系:S=vt。
(2)考点 2:等距离平均速度。
①应用环境:等距离、直线往返、上下坡往返。
②等距离平均速度=2v1v2/(v1+v2)。
2.相对行程:
(1)相遇:S 和=V 和*T。
①直线上:两端相向而行。
②环形上:同点背向而行,相遇 N 次,S 和=N 圈。
③直线多次:两端相向而行,相遇 N 次,S 和=(2N-1)S 单程。
④直线多次:同端相向而行,相遇 N 次,S 和=2NS 单程。
(2)追及:S 差=V 差*T。
①直线上:两端同向而行。
②环形上:同点同向而行,追上 N 次,S 差=n 圈。
(3)流水行船:
①v 顺水=v 船+v 水;v 逆水=v 船-v 水;v 船=(v 顺水+v 逆水)/2;v 水=(v 顺水-v 逆水)/2。
②静水速度=船速、漂流速度=水速。
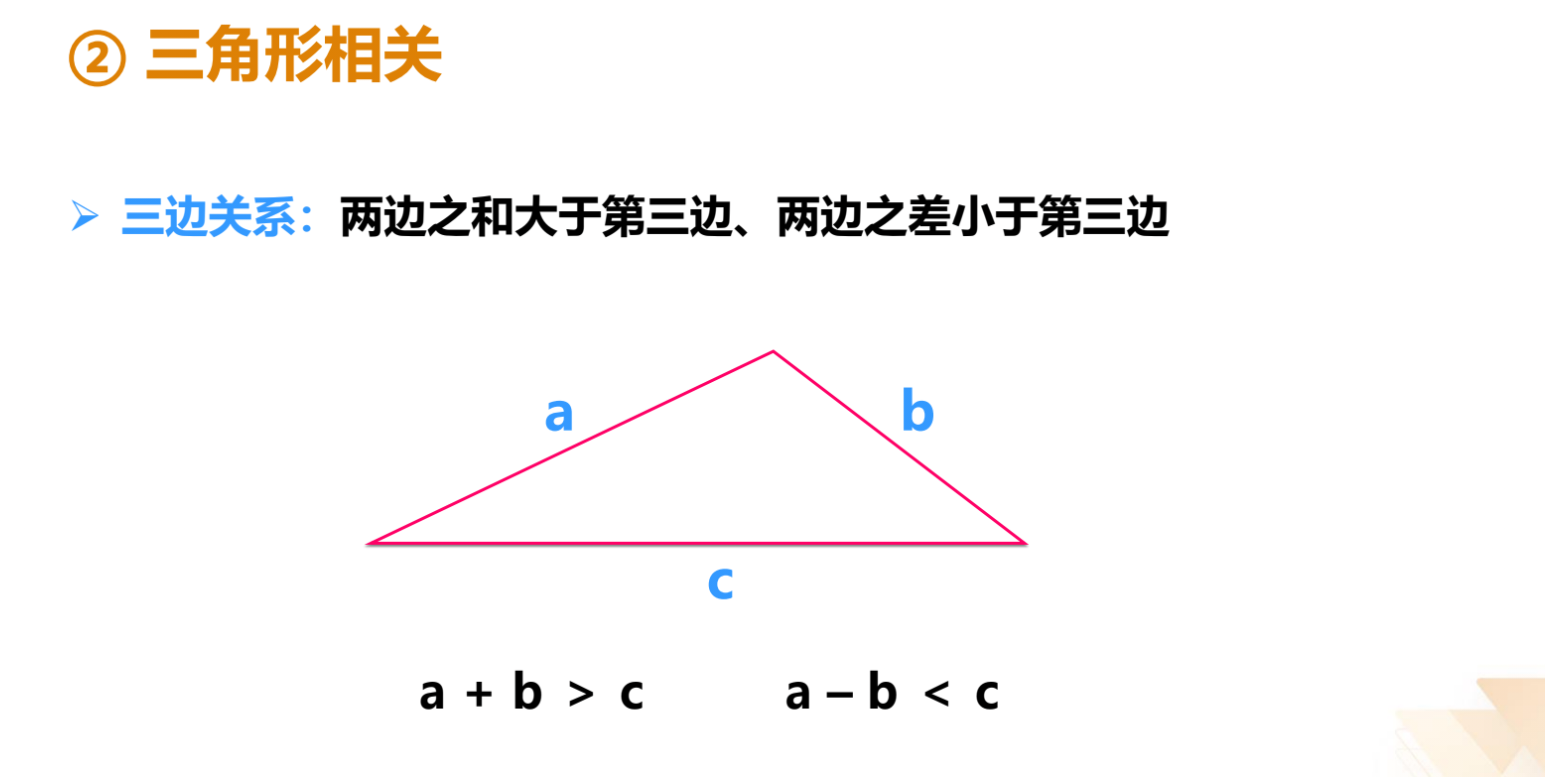
五、几何问题

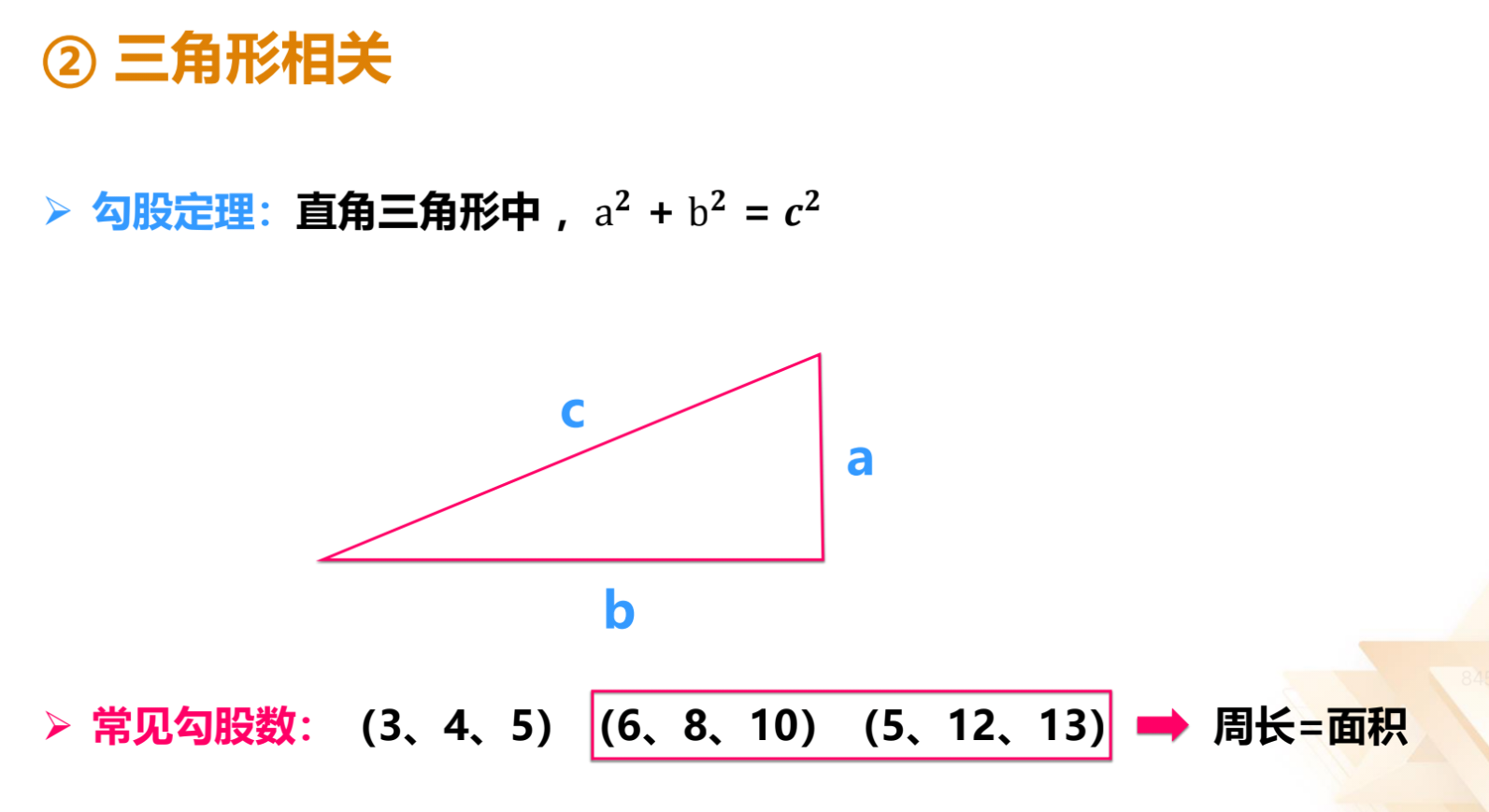

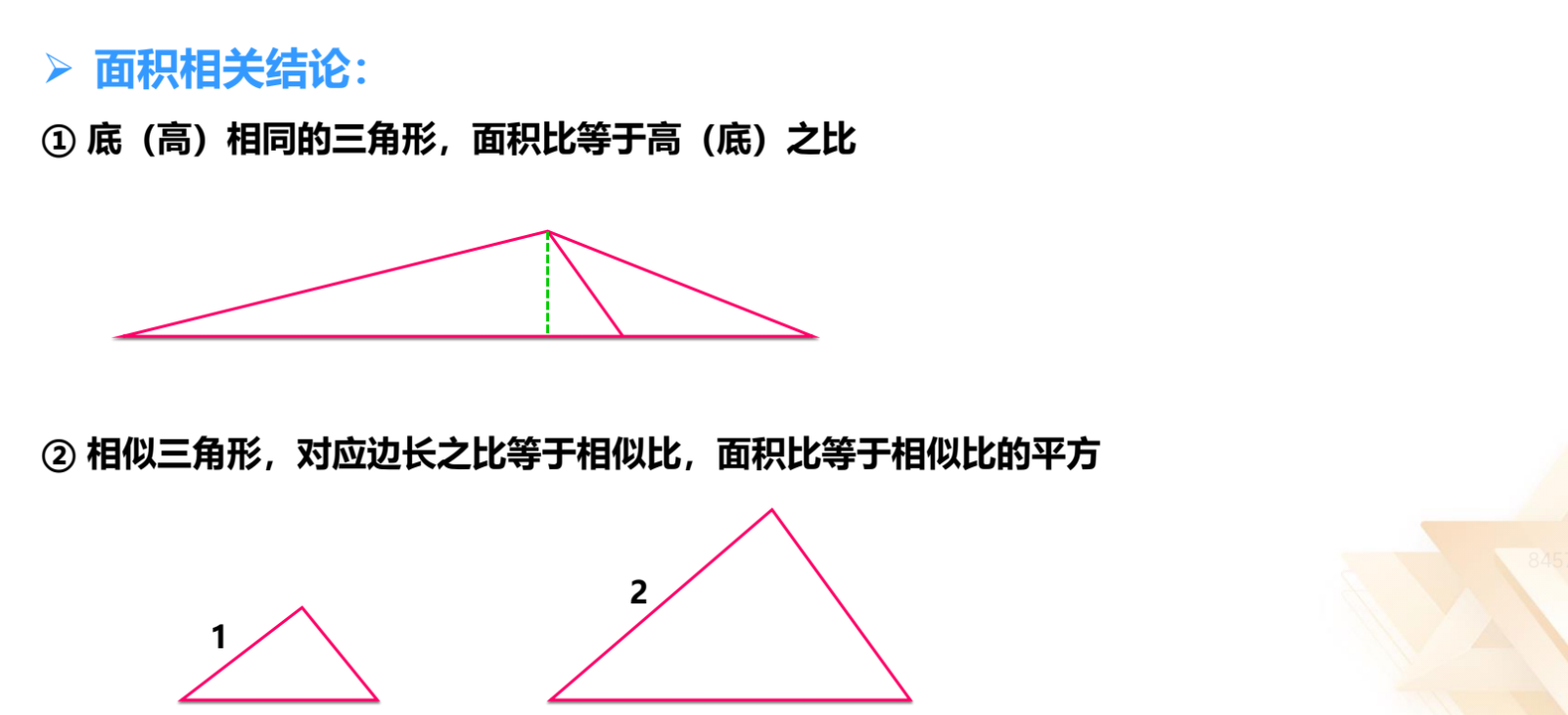
六、排列组合及概率问题
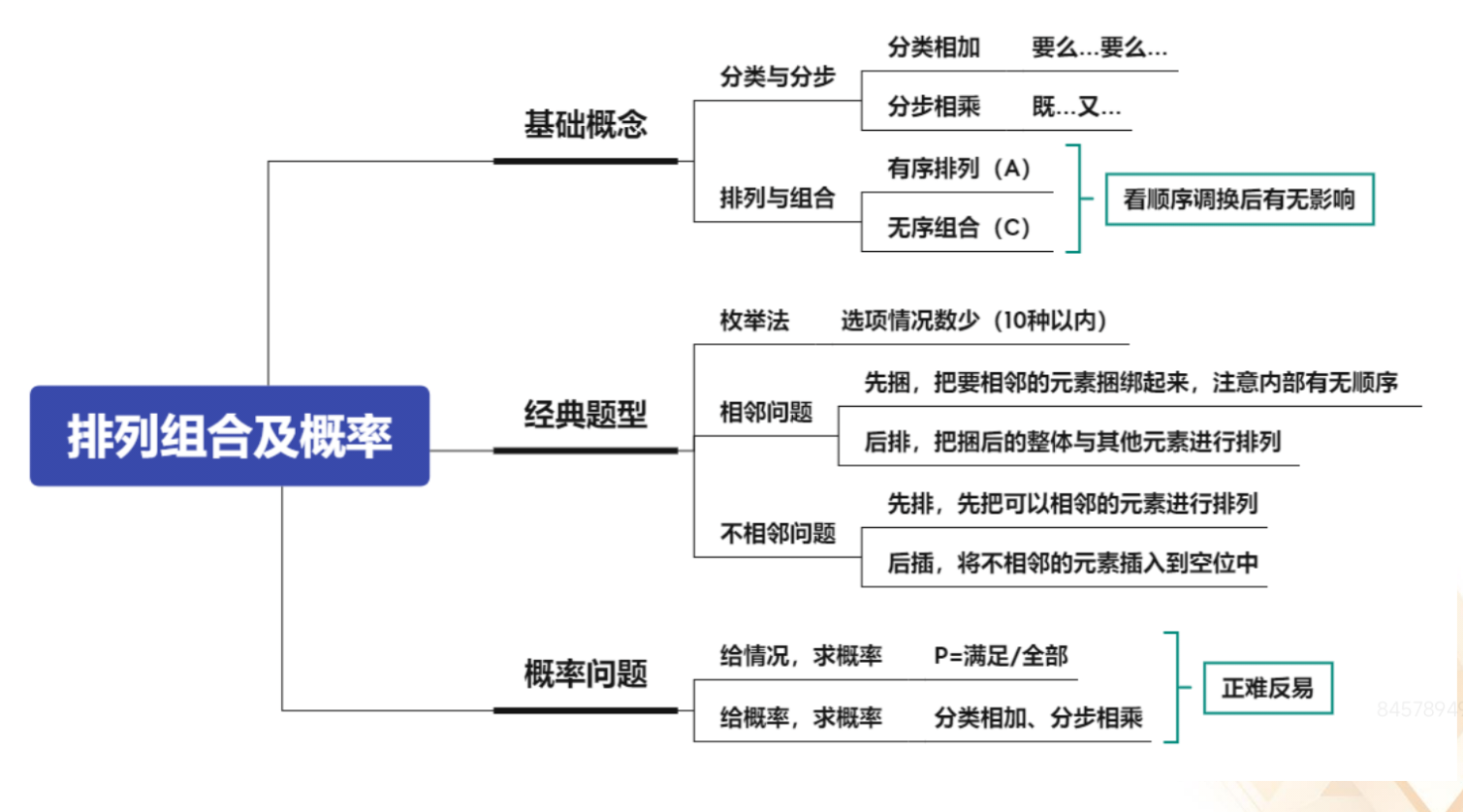
1.基础概念:
(1)分类与分步:
①分类相加:要么„„要么„„。
②分步相乘:既„„又„„。
(2)排列与组合:看顺序调换后有无影响。如:从 4 个人中选 2 个人组成
学习小组,先挑谁后挑谁对结果没有影响,用 C(4,2),从 4 个人中选 2 个人,
一个人打扫卫生一个人学习,谁先选出来谁打扫卫生,对结果有影响,不能用 C,
用 A(4,2)。
①有序排列(A)。
②无序组合(C)。
2.经典题型:
(1)枚举法:选项情况数少(10 种以内)。
(2)相邻问题:如:有五个人,A、B 要挨着,那么把 A、B 捆一起,考虑
内部关系用 A(2,2),再和另外三个人排列,为 A(2,2)*A(4,4)。
①先捆,把要相邻的元素捆绑起来,注意内部有无顺序。
②后排,把捆后的整体与其他元素进行排列。
(3)不相邻问题:如:有五个人,A、B 不相邻,则先把相邻的 3 个人排列,
为 A(3,3),3 个人产生了 4 个空,4 个空中选 2 个排就可以,A(3,3)*A(4,
2)。
①先排,先把可以相邻的元素进行排列。
②后插,将不相邻的元素插入到空位中。
3.概率问题:正难反易,如果正面考虑,情况数大于等于 3 种,那么反面考
虑。
(1)给情况,求概率:P=满足/全部。
(2)给概率,求概率:分类相加、分步相乘。
七、容斥问题
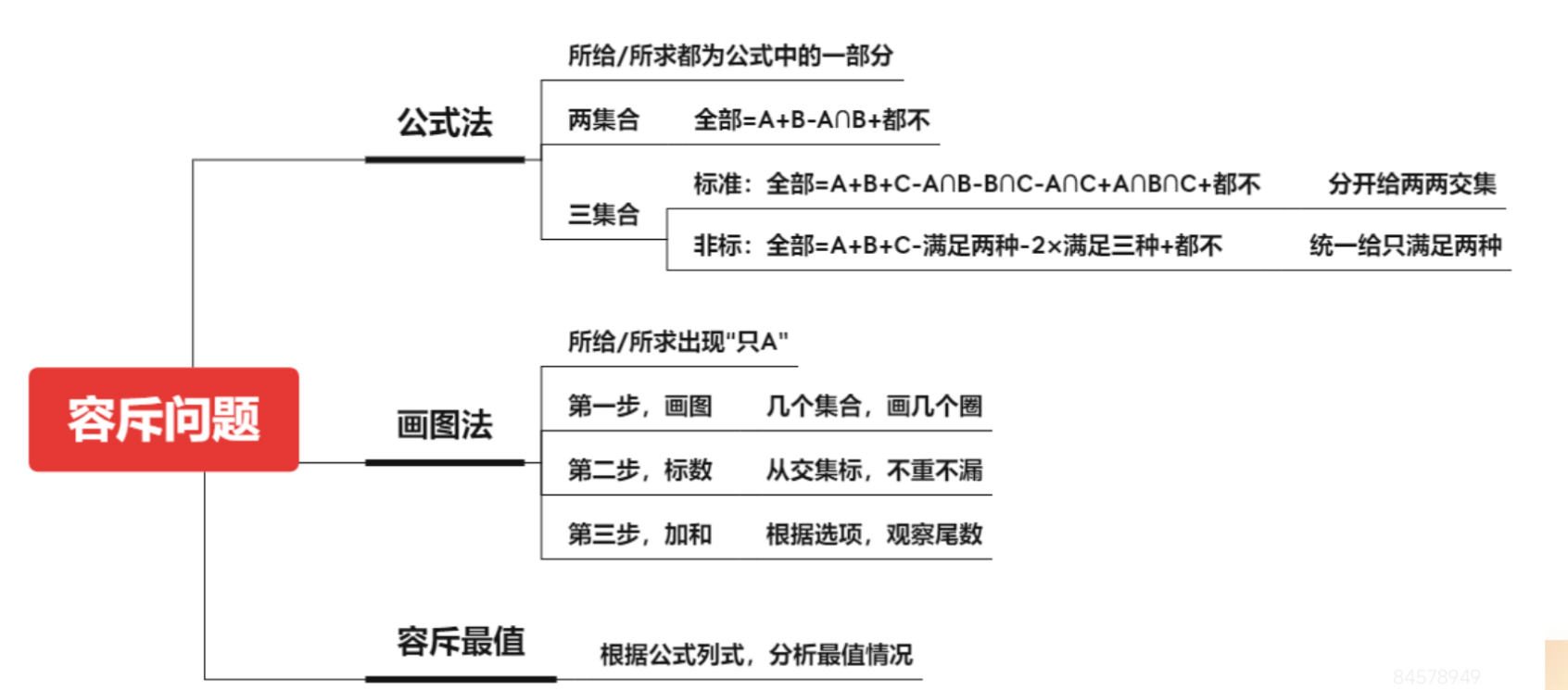
1.公式法:
(1)所给/所求都为公式中的一部分。
(2)两集合:全部=A+B-A∩B+都不。
(3)三集合:
①标准型:全部=A+B+C-A∩B-A∩C-B∩C+A∩B∩C+都不。分开给两两交集。
②非标准型:全部=A+B+C-满足两项-满足三项*2+都不。统一给只满足两种。
2.画图法:所给/所求出现“只 A”。
(1)第一步,画图:几个集合,画几个圈。
(2)第二步,标数:从交集标,不重不漏。
(3)第三步,求和:根据选项,观察尾数。
3.容斥最值:根据公式列式,分析最值情况。














